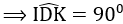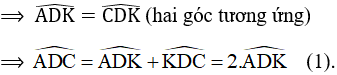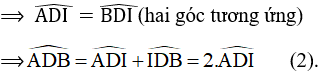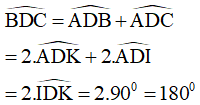- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 1: Tập hợp Q các số hữu tỉ
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 3: Nhân chia số hữu tỉ
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 4: Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Luyện tập trang 15-16
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 5: Lũy thừa của một số hữu tỉ
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-bài 6: Lũy thừa của một số hữu tỉ (tiếp)
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 7: Tỉ lệ thức
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Luyện tập trang 26-27-28
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1- Bài 8 Tính chất của dãy tỉ số bằng nhau
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1- Luyện tập trang 31
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1- Bài 9: Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Luyện tập trang 34-35
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 10: Làm tròn số
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Luyện tập trang 38
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 11: Số vô tỉ. Khái niệm về căn bậc hai
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Bài 12: Số thực
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Luyện tập trang 45
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 1-Ôn tập chương 1
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Bài 1: Đại lượng tỉ lệ thuận
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Bài 2: Một số bài toán về đại lượng tỉ lệ thuận
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Luyện tập trang 56
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2-Bài 3: Đại lượng tỉ lệ nghịch
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2-Bài 4: Một số bài toán về đại lượng tỉ lệ nghịch
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Luyện tập trang 61-62
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2-Bài 5 Hàm số
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Luyện tập trang 64-65
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Bài 6 Mặt phẳng toạ độ
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Luyện tập trang 68
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2- Bài 7: Đồ thị của hàm số y = ax (a ≠ 0)
- Giải bài tập SGK toán 7 tập 1 Phần Đại Số- Chương 2 – Luyện tập trang 72-73-74
- Giải bài tập SGK toán 7 tập 1 – Ôn tập chương 2
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học-Chương 1-Bài 1: Hai góc đối đỉnh
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 82-83
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-bài 2 Hai đường thẳng vuông góc
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 86,87
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Bài 4: Hai đường thẳng song song
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Bài 4: Hai đường thẳng song song
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Bài 5: Tiên đề Ơ-clit về đường thẳng song song
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 94, 95
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Bài 6: Từ vuông góc đến song song
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 98-99
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Bài 7: Định lí
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 101, 102
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 1-Ôn tập chương 1 – Phần Hình học
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Bài 1: Tổng ba góc của một tam giác
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập trang 109
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập trang 109
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập trang 112
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Bài 3: Trường hợp thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập 1 trang 114-115
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2- Luyện tập 2 trang 115-116
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2- Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2- Luyện tập 1 trang 119-120
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập 2 trang 120
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (g.c.g)
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập 1 trang 123-124
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập 2 trang 124
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập về ba trường hợp bằng nhau của tam giác
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Bài 6: Tam giác cân
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập trang 127-128
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-bài 7: Định lí Pi – ta – go
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập 1 trang 131-132
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập 2 trang 133
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Bài 8: Các trường hợp bằng nhau của tam giác vuông
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Luyện tập trang 137
- Giải bài tập SGK toán 7 tập 1 Phần Hình Học – Chương 2-Ôn tập chương 2 – Phần Hình học
- Demo giải bài tập toán lớp 7 sách giáo khoa
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Bài 1: Thu thập số liệu thống kê, tần số
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Luyện tập trang 8-9
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Bài 2: Bảng tần số các giá trị của dấu hiệu
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Luyện tập trang 12
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Bài 3: Biểu đồ
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Luyện tập trang 14-15
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Bài 4: Số trung bình cộng
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3- Luyện tập trang 20-21-22
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 3-Ôn tập chương III
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 1: Khái niệm về biểu thức đại số
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 2: Giá trị của một biểu thức đại số
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 3: Đơn thức
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 4: Đơn thức đồng dạng
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Luyện tập trang 36
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 5: Đa thức
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 6: Cộng, trừ đa thức
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Luyện tập trang 40-41
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 7: Đa thức một biến
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 8: Cộng, trừ đa thức một biến
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Luyện tập trang 46
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Bài 9: Nghiệm của đa thức một biến
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Chương 4-Ôn tập chương IV
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 56 tập 2
- Chương 3-Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 59-60
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 63-64
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Bài 4: Tính chất ba đường trung tuyến của tam giác
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 67
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Bài 5: Tính chất tia phân giác của một góc
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 70-71
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3- Bài 6: Tính chất ba đường phân giác của tam giác
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 73
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3- Bài 7: Tính chất đường trung trực của một đoạn thẳng
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Luyện tập trang 76-77
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Bài 8: Tính chất ba đường trung trực của tam giác
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3- Luyện tập trang 80
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3- Bài 9: Tính chất ba đường cao của tam giác
- Giải bài tập SGK toán 7 tập 2 Phần Hình học- Chương 3-Ôn tập chương III
- Giải bài tập SGK toán 7 tập 2 Phần Hình học-Bài tập Ôn cuối năm Phần Hình Học
- Giải bài tập SGK toán 7 tập 2 Phần Đại số- Bài tập Ôn cuối năm Phần Đại Số
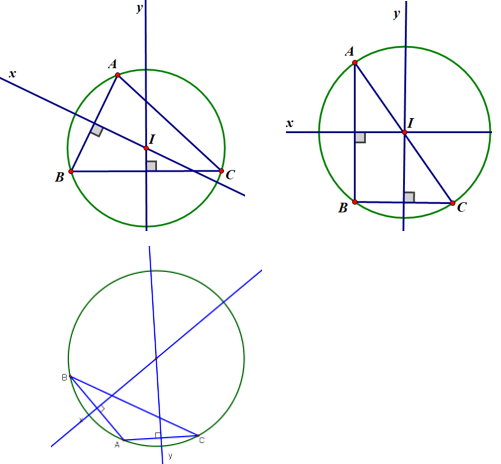
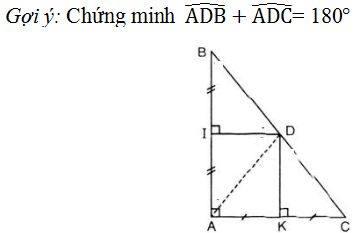
Bài 54 (trang 80 SGK Toán 7 tập 2): Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong các trường hợp sau:
Lời giải:
Đường tròn đi qua ba đỉnh của tam giác ABC gọi là đường tròn ngoại tiếp tam giác đó.
Để vẽ đường tròn ta cần:
+ Vẽ đường trung trực y của cạnh BC.
+ Vẽ dường trung trực x của cạnh AB.
+ x cắt y tại I là tâm của đường tròn cần vẽ.
+ Vẽ đường tròn tâm I bán kính IA.
Nhận xét:
– Tam giác nhọn có tâm đường tròn ngoại tiếp nằm trong tam giác.
– Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền (chứng minh bài 56).
– Tam giác tù có tâm đường tròn ngoại tiếp nằm ngoài tam giác.
Kiến thức áp dụng
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Bài 55 (trang 80 SGK Toán 7 tập 2): Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.
Hình 51
Từ hình vẽ ta có:
+ DK là đường trung trực của AC ⇒ DA = DC.
+ DI là đường trung trực của AB ⇒ DA = DB.
+ Ta có : DI // AC (vì cùng ⏊ AB)
Mà DK ⏊ AC ⇒ DK ⏊ DI
+ Xét ∆ADK và ∆CDK có:
AD = DC
AK = CK (gt)
DK chung
⇒ ∆ADK = ∆CDK (c.c.c)
+ Xét ∆ADI và ∆BDI có :
AD = BD
AI = BI (gt)
DI chung
⇒ ∆ADI = ∆BDI (c.c.c)
Từ (1) và (2) suy ra
Vậy B, D, C thẳng hàng.
Kiến thức áp dụng
+ Điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+ Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
+ Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì sẽ vuông góc với đường thẳng còn lại.
+ Muốn chứng minh 3 điểm thẳng hàng ta chứng minh góc tạo bởi ba điểm đó bằng 1800.
Bài 56 (trang 80 SGK Toán 7 tập 2): Sử dụng bài 55 để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
Lời giải:
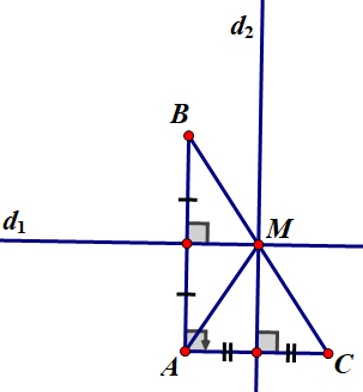
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của BC ⇒ MA đồng thời là trung tuyến của tam giác ABC.
mà MA = MB = MC = (MB + MC)/2 = BC/2.
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
Kiến thức áp dụng
Dựa vào định lí : Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
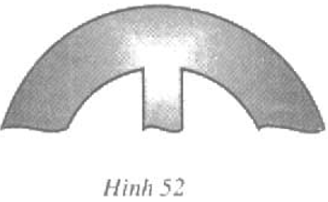
Bài 57 (trang 80 SGK Toán 7 tập 2): Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy. Làm thế nào để xác định được bán kính của đường viền này?
Lời giải:
Để xác định được bán kính ta cần xác định được tâm của đường tròn chứa chi tiết máy này. Ta xác định tâm như sau:
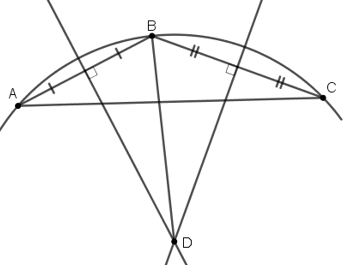
+ Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
+ Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại D. Khi đó D là tâm cần xác định.
+ Bán kính đường tròn cần tìm là độ dài đoạn DB (hoặc DA hoặc DC).
Ta có hình vẽ minh họa