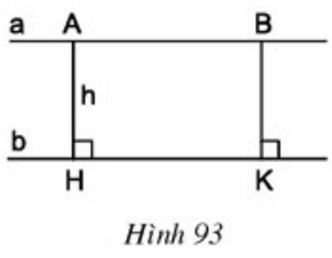
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 100: Cho hai đường thẳng song song a và b (h.93).

Gọi A và B là hai điểm bất kì thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h.

Lời giải

AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành

⇒ AH = BK = h

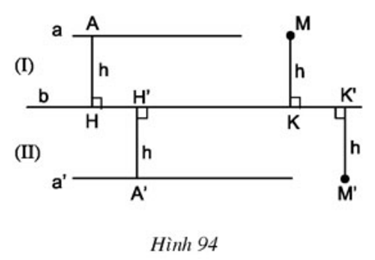
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 101: Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng M ∈ a, M’ ∈ a’.

Lời giải

Góc AHH’ = góc HH’A’ (= 90^o). Mà 2 góc đó là 2 góc so le trong

⇒ a // b

Và a // a’

⇒ a’ // b

– Tứ giác AMKH có AH = MK (= h) và AH // MK (cùng ⊥ b)

⇒ Tứ giác AMKH là hình bình hành ⇒ AM // HK

Mà a // b ⇒ a // HK

Do đó AM trùng với a hay M ∈ a

– Chứng minh tương tự: M’ ∈ a’

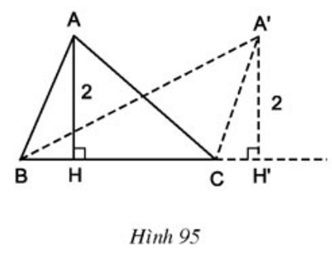
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 101: Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào ?

Lời giải

Đỉnh A của các tam giác đó nằm trên đường thẳng song song với BC và cách BC một khoảng bằng 2 cm

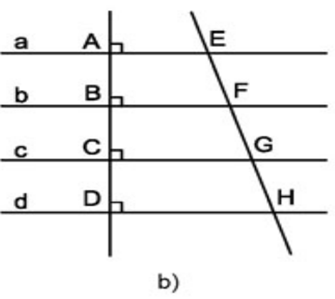
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 102: Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.

Chứng minh rằng:

a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.

b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.

Lời giải

a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD

⇒ B là trung điểm của AC; C là trung điểm của BD

– Hình thang AEGC (AE // GC) có B là trung điểm của AC và BF song song hai cạnh đáy

⇒ F là trung điểm EG (định lí đường trung bình của hình thang)

⇒ EF = FG

– Chứng minh tương tự ⇒ G là trung điểm FH

⇒ FG = GH

Vậy EF = FG = GH

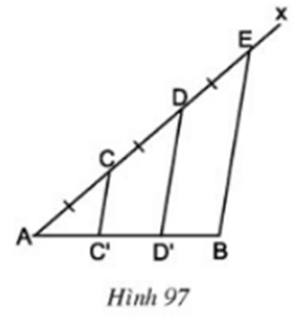
Bài 67 (trang 102 SGK Toán 8 Tập 1): Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

Lời giải:

Ta có: EB // DD’ // CC’ và AC = CD = DE.

Nên theo định lí về các đường thẳng song song cách đều ta suy ra AC’ = C’D’ = D’B

Vậy đoạn thẳng AB bị chia ra ba phần bằng nhau.

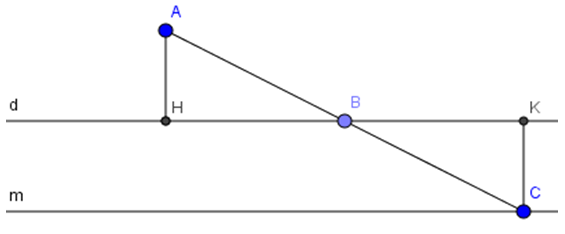
Bài 68 (trang 102 SGK Toán 8 Tập 1): Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?

Lời giải:

Kẻ AH và CK vuông góc với d.

Ta có AB = CB (gt)

Nên ΔAHB = ΔCKB (cạnh huyền – góc nhọn)

Suy ra CK = AH = 2cm

Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.

Bài 69 (trang 103 SGK Toán 8 Tập 1): Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng.

(1) Tập hợp các điểm cách A cố định một khoảng 3cm. (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm.

(5) Là đường trung trực của đoạn thẳng AB. (6) là hai đường thẳng song song với a và cách a một khoảng 3cm. (7) là đường tròn tâm A bán kính 3cm. (8) là tia phân giác của góc xOy

Lời giải:

Ghép các ý:

(1) với (7)

(2) với (5)

(3) với (8)

(4) với (6)