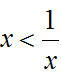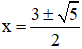Để xem lời giải chi tiết SGK lớp 3,4,5,6,7,8,9,10,11,12 vui lòng truy cập website : edusmart.vn

 

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 4: Nhìn vào hai bức tranh ở trên, hãy đọc và so sánh các câu ở bên trái và bên phải.

Lời giải

Các câu ở bên trái là các câu khẳng định, có tính đúng sai

Các câu ở bên phải không thể nói là đúng hay sai

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 4: Nêu ví dụ về những câu là mệnh đề và những câu không là mệnh đề.

Lời giải

VD về câu là mệnh đề:

5 là số nguyên tố

Sắt là kim loại.

VD về câu không phải là mệnh đề:

Hôm nay là thứ mấy?

Trời đẹp quá!

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 5: Xét câu “x > 3”. Hãy tìm hai giá trị thực của x để từ câu đã cho, nhận được một mệnh đề đúng và một mệnh đề sai.

Lời giải

Với x = 5, mệnh đề nhận được là mệnh đề đúng

Với x =1, mệnh đề nhận được là mệnh đề sai

Các bài giải bài tập Toán 10 Đại số khác:

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 6: Hãy phủ định các mệnh đề sau:

P: “ π là một số hữu tỉ”;

Q: “Tổng hai cạnh của một tam giác lớn hơn cạnh thứ ba”.

Xét tính đúng sai của các mệnh đề trên và mệnh đề phủ định của chúng.

Lời giải

Mệnh đề P: là mệnh đề sai

Mệnh đề phủ định P: “ π không là một số hữu tỉ”;

Mệnh đề Q: là mệnh đề đúng

Mệnh đề phủ định Q: “Tổng hai cạnh của một tam giác không lớn hơn cạnh thứ ba”.

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 6: Từ các mệnh đề:

P: “Gió mùa Đông Bắc về”

Q: “Trời trở lạnh”

Hãy phát biểu mệnh đề P ⇒ Q

Lời giải

P ⇒ Q: “ nếu gió mùa Đông Bắc về thì trời trở lạnh.”

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 7: Cho tam giác ABC. Từ các mệnh đề

P: “Tam giác ABC có hai góc bằng 60^o ”

Q: “ABC là một tam giác đều”

Hãy phát biểu định lí P ⇒ Q. Nêu giả thiết, kết luận và phát biểu lại định lí này dưới dạng điều kiện cần, điều kiện đủ.

Lời giải

P ⇒ Q: “ Nếu tam giác ABC có hai góc bằng 60^o thì ABC là một tam giác đều”

Giả thiết: “Tam giác ABC có hai góc bằng 60^o ”

Kết luận: “ABC là một tam giác đều”

Phát biểu lại định lí này dưới dạng điều kiện cần: “ABC là một tam giác đều là điều kiện cần để tam giác ABC có hai góc bằng 60^o”

Phát biểu lại định lí này dưới dạng điều kiện đủ : “Tam giác ABC có hai góc bằng 60^o là điều kiện đủ để ABC là tam giác đều”

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 7: Cho tam giác ABC. Xét các mệnh đề dạng P ⇒ Q sau

a)Nếu ABC là một tam giác đều thì ABC là một tam giác cân.

b)Nếu ABC là một tam giác đều thì ABC là một tam giác cân và có một góc bằng 60^o

Hãy phát biểu các mệnh đề Q ⇒ P tương ứng và xét tính đúng sai của chúng.

Lời giải

a) Nếu ABC là một tam giác cân thì ABC là tam giác đều

Đây là mệnh đề sai

b) Nếu ABC là một tam giác cân và có một góc bằng 60^o thì ABC là một tam giác đều

Đây là mệnh đề đúng

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 8: Phát biểu thành lời mệnh đề sau:

∀n ∈ Z : n + 1 > n

Mệnh đề này đúng hay sai ?

Lời giải

Với mọi n thuộc tập số nguyên, n + 1 lớn hơn n

Mệnh đề này đúng

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 8: Phát biểu thành lời mệnh đề sau:

∃ x ∈ Z : x² = x

Mệnh đề này đúng hay sai ?

Lời giải

Tồn tại số x thuộc tập số nguyên sao cho x bình phương bằng x

Mệnh đề này đúng vì 0 ∈ Z; 0² = 0

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 8: Hãy phát biểu mệnh đề phủ định của mệnh đề sau

P: “Mọi động vật đều di chuyển được”.

Lời giải

“Tồn tại động vật không di chuyển được”

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 9: Hãy phát biểu mệnh đề phủ định của mệnh đề sau

P: “Có một học sinh của lớp không thích học môn Toán”.

Lời giải

“Tất cả học sinh của lớp đều thích học môn Toán”

Bài 1 (trang 9 SGK Đại số 10): Trong các câu sau, câu nào là mệnh đề, câu nào là mệnh đề chứa biến?

a) 3 + 2 = 7 ;         b) 4 + x = 3;

c) x + y > 1 ;         d) 2 – √5 < 0

Lời giải:

a) 3 + 2 = 7 là mệnh đề sai

Vì 3 + 2 = 5 ≠ 7

b) 4 + x = 3 là mệnh đề chứa biến

Vì với mỗi giá trị của x ta được một mệnh đề.

c) x + y > 1 là mệnh đề chứa biến

Vì với mỗi cặp giá trị của x, y ta được một mệnh đề.

d) 2 – √5 < 0 là mệnh đề đúng

Vì 2 – √5 = √4 – √5 < 0 đúng

Bài 2 (trang 9 SGK Đại số 10): Xét tính đúng sai của mỗi mệnh đề sau và phát biểu mệnh đề phủ định của nó:

a) 1794 chia hết cho 3 ;         b) √2 là một số hữu tỉ

c) π < 3, 15 ;         d) |-125| ≤ 0

Lời giải:

a) Mệnh đề đúng vì 1794 : 3 = 598

Mệnh đề phủ định: “1794 không chia hết cho 3”

b) Mệnh đề sai vì √2 là số vô tỉ

Mệnh đề phủ định: “√2 không phải là một số hữu tỉ”

c) Mệnh đề đúng

Mệnh đề phủ định: “π ≥ 3, 15”

d) Mệnh đề sai vì |-125| = 125 > 0

Mệnh đề phủ định: “|-125| > 0”

Bài 3 (trang 9 SGK Đại số 10): Cho các mệnh đề kéo theo:

Nếu a và b cùng chia hết cho c thì a + b chia hết cho c (a, b, c là những số nguyên).

Các số nguyên tố có tận cùng bằng 0 đều chia hết cho 5.

Một tam giác cân có hai đường trung tuyến bằng nhau.

Hai tam giác bằng nhau có diện tích bằng nhau.

a) Hãy phát biểu mệnh đề đảo của mỗi mệnh đề trên.

b) Hãy phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái nieemh “điều kiện đủ”.

c) Phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm “điều kiện cần”.

Lời giải:

a)

+ Nếu a + b chia hết cho c thì a và b chia hết cho c.

+ Các số nguyên chia hết cho 5 thì có tận cùng bằng 0.

+ Nếu một tam giác có hai trung tuyến bằng nhau thì tam giác đó cân.

+ Nếu hai tam giác có diện tích bằng nhau thì bằng nhau.

b)

+ a và b chia hết cho c là điều kiện đủ để a + b chia hết cho c.

+ Một số tận cùng bằng 0 là điều kiện đủ để số đó chia hết cho 5.

+ Tam giác cân là điều kiện đủ để tam giác đó có hai đường trung tuyến bằng nhau.

+ Hai tam giác bằng nhau là điều kiện đủ để hai tam giác đó có diện tích bằng nhau.

c)

+ Điều kiện cần để a và b chia hết cho c là a + b chia hết cho c.

hoặc “a + b chia hết cho c là điều kiện cần để a và b chia hết cho c.”

+ Các số nguyên chia hết cho 5 là điều kiện cần để số đó có tận cùng bằng 0.

+ Điều kiện cần để tam giác cân là tam giác đó có hai đường trung tuyến bằng nhau.

hoặc “Hai trung tuyến của một tam giác bằng nhau là điều kiện cần để tam giác đó cân.”

+ Hai tam giác có diện tích bằng nhau là điều kiện cần để hai tam giác đó bằng nhau.

Bài 4 (trang 9 SGK Đại số 10): Phát biểu mỗi mệnh đề sau, bằng cách sử dụng khái niệm “điều kiện cần và đủ”.

a) Một số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và ngược lại.

b) Một hình bình hành có các đường chéo vuông góc là một hình thoi và ngược lại.

c) Phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương.

Lời giải:

a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.

b) Một hình bình hành có các đường chéo vuông góc là điều kiện cần và đủ để nó là một hình thoi.

c) Để phương trình bậc hai có hai nghiệm phân biệt, điều kiện cần và đủ là biệt thức của nó dương.

Bài 5 (trang 10 SGK Đại số 10): Dùng kí hiệu ∀, ∃ để viết các mệnh đề sau:

a) Mọi số nhân với 1 đều bằng chính nó.

b) Có một số cộng với chính nó bằng 0.

c) Mọi số cộng với số đối của nó đều bằng 0.

Lời giải:

a) ∀ x ∈ R: x.1 = x

b) ∃ a ∈ R: a + a = 0

c) ∀ x ∈ R: x + (-x) = 0

Bài 6 (trang 10 SGK Đại số 10): Phát biểu thành lời mỗi mệnh đề sau và xét tính đúng sai của nó.

a) ∀ x ∈ R : x² > 0 ;             b) ∃ n ∈ N : n² = n

Lời giải:

a) Bình phương của mọi số thực đều là số dương.

– Mệnh đề này sai vì nếu x = 0 thì x² = 0.

Sửa cho đúng: ∀ x ∈ R : x² ≥ 0.

b) Tồn tại ít nhất một số tự nhiên n sao cho n² = n.

– Mệnh đề này đúng (ví dụ: n = 0; n = 1).

c) Với mọi số tự nhiên n ta có: n ≤ 2n.

– Mệnh đề này đúng.

d) Có một số thực x sao cho

– Mệnh đề này đúng.

Bài 7 (trang 10 SGK Đại số 10): Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó:

a) ∀ n ∈ N: n chia hết cho n ;        b) ∃ x ∈ Q : x² = 2

c) ∀ x ∈ R : x < x + 1 ;        d) ∃ x ∈ R: 3x = x² + 1

Lời giải:

a) ∃ n ∈ N: n không chia hết cho n.

Mệnh đề phủ định đúng.

b) ∀ x ∈ Q : x² ≠ 2

Mệnh đề phủ định đúng.

c) ∃ x ∈ R: x ≥ x + 1.

Mệnh đề phủ định sai (vì x ≥ x + 1 ⇒ 0 ≥ 1 sai)

d) ∀ x ∈ R ; 3x ≠ x² + 1

Mệnh đề phủ định sai vì