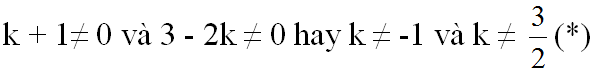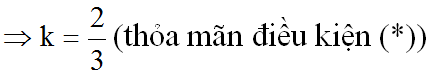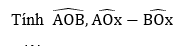- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 2: Căn thức bậc hai và hằng đẳng thức
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Luyện tập trang 9
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 3: Liên hệ giữa phép nhân và phép khai phương
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Luyện tập trang 15-16 (Tập 1)
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 4: Liên hệ giữa phép chia và phép khai phương
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1- Luyện tập trang 19-20 (Tập 1)
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 5: Bảng căn bậc hai
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Luyện tập trang 30
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 8: Rút gọn biểu thức chứa căn thức bậc hai
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Luyện tập (trang 33-34)
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Bài 9: Căn bậc ba
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 1-Ôn tập chương 1 phần Đại số
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2 – Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Luyện tập trang 45-46
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Bài 2: Hàm số bậc nhất
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Luyện tập trang 48
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2- Bài 3: Đồ thị của hàm số y = ax + b
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Luyện tập trang 51-52
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Bài 4: Đường thẳng song song và đường thẳng cắt nhau
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Luyện tập trang 55
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Bài 5: Hệ số góc của đường thẳng y = ax + b
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Luyện tập trang 59
- Giải bài tập SGK toán 9 tập 1 Phần Đại Số – Chương 2-Ôn tập chương 2 phần Đại số
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1- Luyện tập trang 69-70 Kì 1
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Bài 2: Tỉ số lượng giác của góc nhọn
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 77
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Bài 3: Bảng lượng giác
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 84
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 89
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học – Chương 1-Ôn tập chương 1 phần Hình học
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Luyện tập trang 100-101
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 2: Đường kính và dây của đường tròn
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Luyện tập trang 106
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 4: Vị trí tương đối của đường thẳng và đường tròn
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Luyện tập trang 111
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 6: Tính chất của hai tiếp tuyến cắt nhau
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Luyện tập trang 116
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 7: Vị trí tương đối của hai đường tròn
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Luyện tập trang 123
- Giải bài tập SGK toán 9 tập 1 Phần Hình Học- Chương 2-Ôn tập chương 2 phần Hình học
- Test post
- Test Post 2
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Bài 1: Phương trình bậc nhất hai ẩn
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Bài 2: Hệ hai phương trình bậc nhất hai ẩn
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Luyện tập trang 12
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Bài 3: Giải hệ phương trình bằng phương pháp thế
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Luyện tập trang 15-16
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Luyện tập trang 19-20 (Tập 2)
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Bài 5: Giải bài toán bằng cách lập hệ phương trình
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Bài 6: Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Luyện tập trang 24-25
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 3-Ôn tập chương 3 (Câu hỏi – Bài tập)
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 1: Hàm số y = ax2 (a ≠ 0)
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Luyện tập trang 38-39
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 3: Phương trình bậc hai một ẩn
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 4: Công thức nghiệm của phương trình bậc hai
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4- Bài 5: Công thức nghiệm thu gọn
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Luyện tập trang 49-50
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 6: Hệ thức Vi-ét và ứng dụng
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Luyện tập trang 54
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 7: Phương trình quy về phương trình bậc hai
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Luyện tập trang 56-57
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài 8: Giải bài toán bằng cách lập phương trình
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4- Luyện tập trang 59-60
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4- Ôn tập chương 4 (Câu hỏi – Bài tập)
- Giải bài tập SGK toán 9 tập 2 Phần Đại Số – Chương 4-Bài tập ôn cuối năm
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 1: Góc ở tâm. Số đo cung
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 69-70 Kì 2
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 2: Liên hệ giữa cung và dây
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 3: Góc nội tiếp
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 75-76
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 79-80
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 83
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 6: Cung chứa góc
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 87
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 87
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 7: Tứ giác nội tiếp
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Luyện tập trang 89-90
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 9: Độ dài đường tròn, cung tròn
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3- Luyện tập trang 95-96
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Bài 10: Diện tích hình tròn, hình quạt tròn
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3- Luyện tập trang 99-100
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 3-Ôn tập chương 3 phần Hình Học
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Bài 1: Hình Trụ – Diện tích xung quanh và thể tích của hình trụ
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4- Luyện tập trang 111-112-113
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Bài 2: Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Luyện tập trang 119-120
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Luyện tập trang 126
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Ôn tập chương 4 phần Hình Học
- Giải bài tập SGK toán 9 tập 2 Phần Hình học – Chương 4-Bài tập ôn cuối năm-Phần Hình Học
Bài 1 (trang 59 SGK Toán 9 Tập 1): Cho hàm số y = ax = b (a ≠ 0).
a) Khi nào thì hàm số đồng biến?
b) Khi nào thì hàm số nghịch biến?
Trả lời:
a) Hàm số đồng biến khi a > 0
b) Hàm số nghịch biến khi a < 0
Bài 2 (trang 60 SGK Toán 9 Tập 1): Khi nào thì hai đường thẳng y = ax + b ( a ≠ 0) và y = a’x + b’ (a’ ≠ 0) cắt nhau? Song song với nhau? Trùng nhau?
Trả lời:
Hai đường thẳng y = ax + b và y = a’x + b’ (a, a’ ≠ 0)
– Cắt nhau khi và chỉ khi a ≠ a’
– Song song với nhau khi và chỉ khi a = a’, b ≠ b’
– Trùng nhau khi và chỉ khi a = a’, b = b’
Bài 32 (trang 61 SGK Toán 9 Tập 1): a) Với những giá trị nào của m thì hàm số bậc nhất y = (m – 1)x + 3 đồng biến?
b) Với những giá trị nào của k thì hàm số bậc nhất y = (5 – k)x + 1 nghịch biến?
Lời giải:
a) Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)
Hàm số đồng biến khi m – 1 > 0 hay m > 1.
Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.
b) Hàm số y = (5 – k)x + 1 là hàm số bậc nhất đối với x khi 5 – k ≠ 0 hay k ≠ 5 (**).
Hàm số nghịch biến khi 5 – k < 0 hay k < 5.
Kết hợp với điều kiện (**) ta được với k < 5 thì hàm số nghịch biến.
Bài 33 (trang 61 SGK Toán 9 Tập 1): Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung?
Lời giải:
Đồ thị hai hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung nên ta thay hoành độ x = 0 vào:
hàm số y = 2x + (3 + m) ta được tung độ: y = 3 + m
hàm số y = 3x + (5 – m) ta được tung độ: y = 5 – m
Vì cùng là tung độ của giao điểm nên:
3 + m = 5 – m => m = 1
Vậy khi m = 1 thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.
(Lưu ý: Điểm trên trục tung có hoành độ là 0)
Bài 34 (trang 61 SGK Toán 9 Tập 1): Tìm giá trị của a để hai đường thẳng y = (a – 1)x + 2 (a ≠ 1) và y = (3 – a)x + 1 (a ≠ 3) song song với nhau.
Lời giải:
Theo đề bài ta có b ≠ b’ (vì 2 ≠ 1)
Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:
a – 1 = 3 – a
=> a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)
Vậy với a = 2 thì hai đường thẳng song song với nhau.
Bài 35 (trang 61 SGK Toán 9 Tập 1): Xác định k và m để hai đường thẳng sau đây trùng nhau:
y = kx + (m – 2) (k ≠ 0); y = (5 – k)x + (4 – m) (k ≠ 5)
Lời giải:
Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:
k = 5 – k (1) và m – 2 = 4 – m (2)
Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)
Từ (2) suy ra m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.
Bài 36 (trang 61 SGK Toán 9 Tập 1): Cho hai hàm số bậc nhất y = ( k + 1)x + 3 và y = (3 – 2k)x + 1.
a) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng song song với nhau?
b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau?
c) Hai đường thẳng nói trên có thể trùng nhau được không? Vì sao?
Lời giải:
Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a’ = 3 – 2k, b’ = 1
Hai hàm số là hàm số bậc nhất nên a và a’ khác 0, tức là:
a) Theo đề bài ta có b ≠ b’ (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a’
tức là: k + 1 = 3 – 2k
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 cắt nhau khi a ≠ a’ tức là:
thì hai đường thẳng cắt nhau.
c) Do b ≠ b’ (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.
Bài 37 (trang 61, 62 SGK Toán 9 Tập 1): a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:
y = 0,5x + 2 (1); y = 5 – 2x (2)
b) Gọi giao điểm của các đường thẳng y = 0,5x + 2 và y = 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tìm tọa độ của các điểm A, B, C.
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị đo trên các trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).
Lời giải:
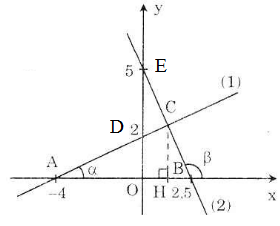
a) – Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
– Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)
Hoành độ giao điểm C của hai đồ thị là nghiệm phương trình:
0,5x + 2 = 5 – 2x => x = 1,2
=> y = 0,5.1,2 + 2 = 2,6
=> Tọa độ C(1,2 ; 2,6)
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
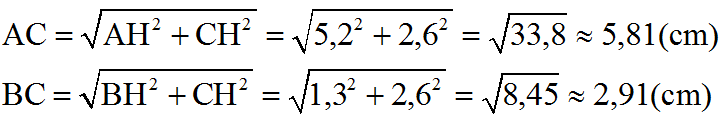
Ta có: tgα = 0,5 => α = 26o34′
Gọi β là góc hợp bởi đường thẳng y = 5 – 2x với tia Ox (β là góc tù).
Gọi β’ là góc kề bù với β, ta có:
tgβ’ = -(-2) = 2 => β’ = 63o26′
=> β = 180o – 63o26′ = 116o34′
Bài 38 (trang 62 SGK Toán 9 Tập 1): a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
Hướng dẫn câu c)
Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
Lời giải:
a) – Vẽ đồ thị y = 2x (1):
Cho x = 0 => y = 0 được O
Cho x = 1 => y = 2 được điểm (1; 2)
– Vẽ đồ thị y = 0,5x (2):
Cho x = 0 => y = 0 được O
Cho x = 2 => y = 1 được điểm (2; 1)
– Vẽ đồ thị y = -x + 6 (3):
Cho x = 0 => y = 6 được điểm (0; 6)
Cho y = 0 => x = 6 được điểm (6; 0)
b) Theo đề bài A, B theo thứ tự là giao điểm của đường thẳng (3) với các đường thẳng (1) và (2), nên ta có:
Hoành độ giao điểm của A là nghiệm của phương trình:
– x + 6 = 2x => x = 2
=> y = 4 => A(2; 4)
Hoành độ giao điểm của B là nghiệm của phương trình:
– x + 6 = 0,5x => x = 4
=> y = 2 => B(4; 2)