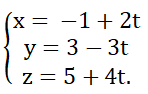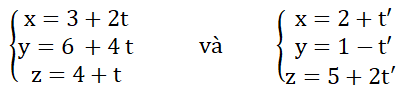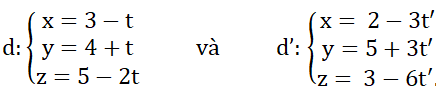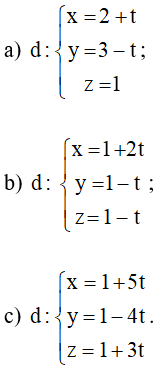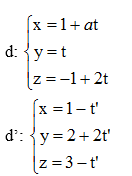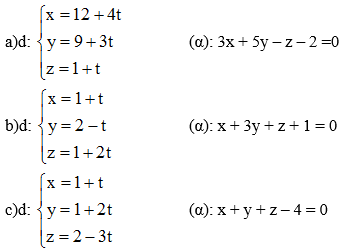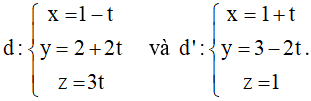- Giải bài tập SGK toán 12 phần giải tích-Chương 1:Bài 1: Sự đồng biến, nghịch biến của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1:Bài 2 cực trị của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1:Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1 Bài 4: Đường tiệm cận
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1: Bài Ôn tập chương 1 Giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1: Bài Ôn tập chương 1 Giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 1: Lũy thừa
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 2: Hàm số lũy thừa
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 3: Lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 4: Hàm số mũ. Hàm số lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 5: Phương trình mũ và phương trình lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 6: Bất phương trình mũ và bất phương trình lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài ôn tập chương 2
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Bài 1 : Nguyên hàm
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Bài 2 : Tích phân
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Bài 3 : Ứng dụng của tích phân trong hình học
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Ôn tập chương 3 giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Ôn tập chương 3 giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 1 : Số phức
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 2 : Cộng, trừ và nhân số phức
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 3 : Phép chia số phức
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 4 : Phương trình bậc hai với hệ số thực
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập chương 4
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập chương 4
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập cuối năm giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập cuối năm giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Bài 1: Khái niệm về khối đa diện
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Bài 2: Khối đa diện lồi và khối đa diện đều
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Bài 3: Khái niệm về thể tích của khối đa diện
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Ôn tập chương 1
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Câu hỏi trắc nghiệm chương I
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Bài 1 : Khái niệm về mặt tròn xoay
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Bài 2 : Mặt cầu
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Ôn tập chương 2 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Câu hỏi trắc nghiệm chương 2 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Bài 1 : Hệ tọa độ trong không gian
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Bài 2 : Phương trình mặt phẳng
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Bài 3 : Phương trình đường thẳng trong không gian
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Ôn tập chương 3 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Câu hỏi trắc nghiệm chương 3 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Ôn tập cuối năm Hình học 12
Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 82: Trong không gian Oxyz cho điểm Mo(1; 2; 3) và hai điểm M1(1 + t; 2 + t; 3 + t), M2(1 + 2t; 2 + 2t; 3 + 2t) di động với tham số t. Hãy chứng tỏ ba điểm Mo,M1,M2 luôn thẳng hàng.
Lời giải:
MoM1→ = (t;t;t); MoM2→ = (2t;2t;2t)
⇒ MoM2→ = 2MoM1→ ⇒ MoM1→ và MoM2→ cùng phương
⇒ ba điểm Mo, M1, M2 luôn thẳng hàng
Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 84: Cho đường thẳng Δ có phương trình tham số
Hãy tìm tọa độ của một điểm M trên Δ và tọa độ một vecto chỉ phương của Δ.
Lời giải:
1 điểm M thuộc Δ là: M (-1; 3; 5) và 1 vecto chỉ phương của Δ là a→ = (2;-3;4)
Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 84: Cho hai đường thẳng d và d’ có phương trình tham số lần lượt là
a) Hãy chứng tỏ điểm M(1; 2; 3) là điểm chung của d và d’;
b) Hãy chứng tỏ d và d’ có hai vecto chỉ phương không cùng phương.
Lời giải:
a) tọa độ M thỏa mãn phương trình tham số của d với t = -1
Tọa độ M thỏa mãn phương trình tham số của d’ với t = -1
⇒ M là điểm chung của d và d’
b) ad→ = (2;4;1); ad’→ = (1;-1;2) là hai vecto không tỉ lệ nên hai veco đó không cùng phương
Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 86: Chứng minh hai đường thẳng sau đây trùng nhau:
Lời giải:
ad→ = (-1;1;-2); ad’→ = (-3;3;-6) ⇒ ad’→ = 3ad→
M (3; 4; 5) ∈ d và M (3; 4; 5) ∈ d’
Nên d trùng với d’
Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 89: Tìm số giao điểm của mặt phẳng (α): x + y + z – 3 = 0 với đường thẳng d trong các trường hợp sau:
Lời giải:
a) Xét phương trình: (2 + t) + (3 – t) + 1 – 3 = 0
⇔ 3 = 0(vô nghiệm) ⇒ mặt phẳng (α)và d không có điểm chung
b) Xét phương trình: (1 + 2t) + (1 – t) + (1 – t) – 3 = 0
⇔ 0 = 0(vô số nghiệm) ⇒ d ∈ (α)
c) Xét phương trình: (1 + 5t) + (1 – 4t) + (1 + 3t) – 3 = 0
⇔ 4t = 0 ⇔ t = 0 ⇒ mặt phẳng (α)và d có 1 điểm chung
Bài 1 (trang 89 SGK Hình học 12): Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
Lời giải:
Bài 2 (trang 89 SGK Hình học 12): Viết phương trình tham số của đường thẳng là hình chiếu vuông góc của đường thẳng
Lời giải:
Bài 3 (trang 90 SGK Hình học 12): Xét vị trí tương đối các cặp đường thẳng d và d’ cho bởi các phương trình sau:
Lời giải:
Bài 4 (trang 90 SGK Hình học 12): Tìm a để hai đường thẳng sau đây cắt nhau:
Lời giải:
Bài 5 (trang 90 SGK Hình học 12): Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
Lời giải:
Bài 6 (trang 90 SGK Hình học 12): Tính khoảng cách giữa đường thẳng …
Lời giải:
Bài 7 (trang 91 SGK Hình học 12): Cho điểm A(1; 0; 0) và đường thẳng …
Lời giải:
Bài 8 (trang 91 SGK Hình học 12): Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0
a)Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
b)Tìm tọa độ điểm M’ đối xứng với M qua mặt phẳng (α).
c)Tính khoảng cách từ M đến mp(α).
Lời giải:
Bài 9 (trang 91 SGK Hình học 12): Cho hai đường thẳng d:
Lời giải:
Bài 10 (trang 91 SGK Hình học 12): Giải bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Tính khoảng cách từ đỉnh A đến các mặt phẳng (A’BD) và (B’D’C).
Lời giải: