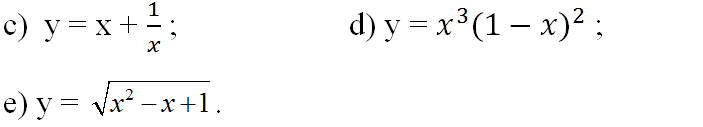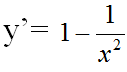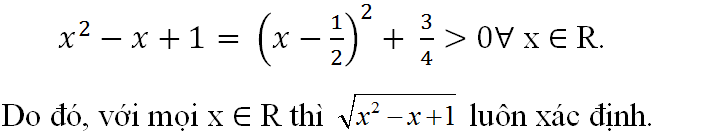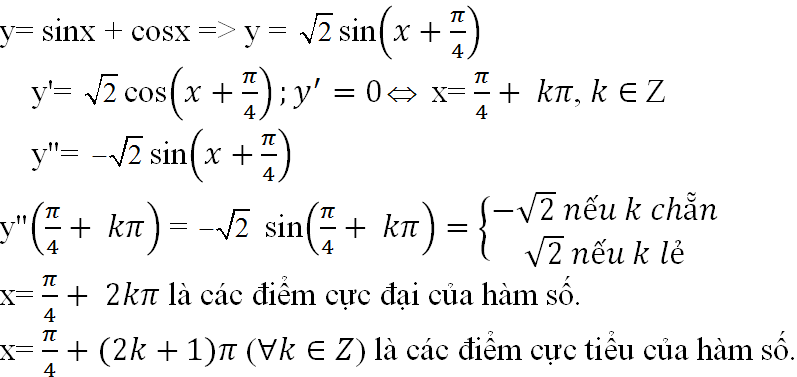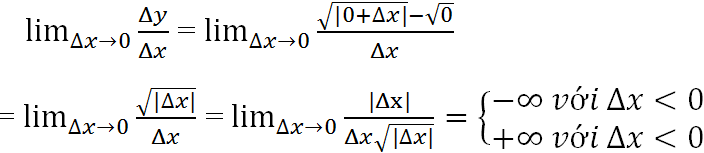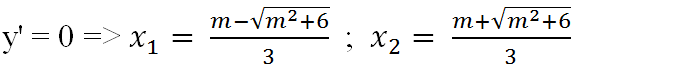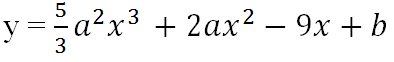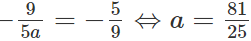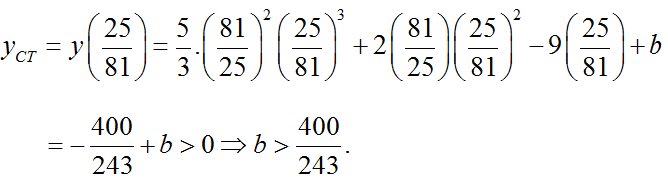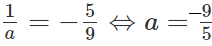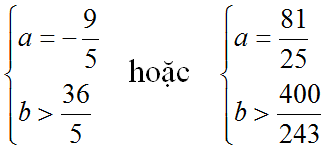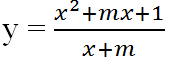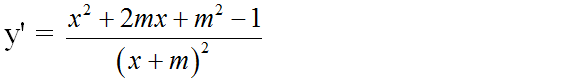- Giải bài tập SGK toán 12 phần giải tích-Chương 1:Bài 1: Sự đồng biến, nghịch biến của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1:Bài 2 cực trị của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1:Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1 Bài 4: Đường tiệm cận
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1: Bài Ôn tập chương 1 Giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12 – CHƯƠNG 1: Bài Ôn tập chương 1 Giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 1: Lũy thừa
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 2: Hàm số lũy thừa
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 3: Lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 4: Hàm số mũ. Hàm số lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 5: Phương trình mũ và phương trình lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài 6: Bất phương trình mũ và bất phương trình lôgarit
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 2 Bài ôn tập chương 2
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Bài 1 : Nguyên hàm
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Bài 2 : Tích phân
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Bài 3 : Ứng dụng của tích phân trong hình học
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Ôn tập chương 3 giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 3 Ôn tập chương 3 giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 1 : Số phức
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 2 : Cộng, trừ và nhân số phức
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 3 : Phép chia số phức
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Bài 4 : Phương trình bậc hai với hệ số thực
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập chương 4
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập chương 4
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập cuối năm giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA GIẢI TÍCH 12-CHƯƠNG 4 Ôn tập cuối năm giải tích 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Bài 1: Khái niệm về khối đa diện
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Bài 2: Khối đa diện lồi và khối đa diện đều
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Bài 3: Khái niệm về thể tích của khối đa diện
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Ôn tập chương 1
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 1 Câu hỏi trắc nghiệm chương I
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Bài 1 : Khái niệm về mặt tròn xoay
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Bài 2 : Mặt cầu
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Ôn tập chương 2 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 2 Câu hỏi trắc nghiệm chương 2 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Bài 1 : Hệ tọa độ trong không gian
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Bài 2 : Phương trình mặt phẳng
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Bài 3 : Phương trình đường thẳng trong không gian
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Ôn tập chương 3 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Câu hỏi trắc nghiệm chương 3 Hình học 12
- GIẢI BÀI TẬP SÁCH GIÁO KHOA HÌNH HỌC 12-CHƯƠNG 3 Ôn tập cuối năm Hình học 12
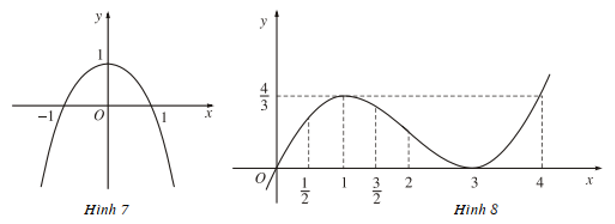
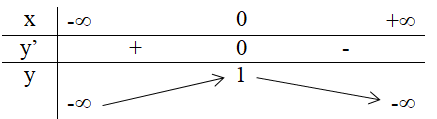
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 13: Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
a) y = -x2 + 1 trong khoảng (-∞; +∞);
b) y = x/3(x+ 3)2 trong các khoảng (1/2; 3/2) và (3/2; 4).
Lời giải:
a) Tại x = 0 hàm số có giá trị lớn nhất bằng 1.
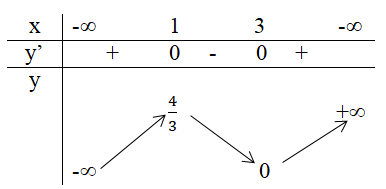
Xét dấu đạo hàm:
b) Tại x = 1 hàm số có giá trị lớn nhất bằng 4/3.
Tại x = 3 hàm số có giá trị nhỏ nhất bằng 0.
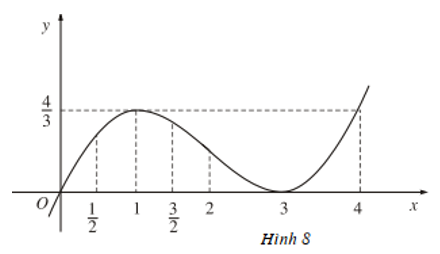
Xét dấu đạo hàm:
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 14: Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số 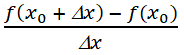
Lời giải:
Với Δx > 0 Ta có 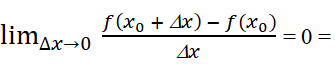
Với Δx < 0 Ta có 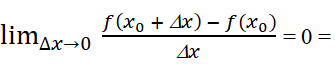
Vậy f’(xo) = 0.
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 14: a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không.
• y = -2x + 1;
• y = x/3(x-3)2 (H.8).
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Lời giải:
a,Hàm số y = -2x + 1 không có cực trị.
Hàm số y = x/3 (x-3)2 đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.
b, Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 16: Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?
Lời giải:
Vậy không tồn tại đạo hàm của hàm số tại x = 0.
Nhưng dựa vào đồ thị của hàm số y = |x|. Ta có hàm số đạt cực trị tại x = 0.
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 16: Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x^2 – 3).
Lời giải:
1. TXĐ: D = R
2. f’(x) = 3x^2 – 3. Cho f’(x) = 0 ⇔ x = 1 hoặc x = -1.
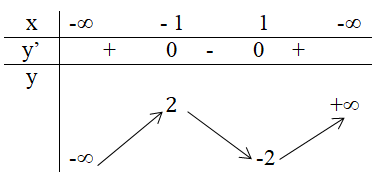
3. Ta có bảng biến thiên:
Hàm số đạt cực đại tại x = -1 và giá trị cực đại là 2
Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là -2.
Bài 1 (trang 18 SGK Giải tích 12): Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
a) y = 2x3 + 3x2 – 36x – 10 ; b) y = x4 + 2x2 – 3;
Lời giải:
a) TXĐ: D = R
y’ = 6x2 + 6x – 36 = 6(x2 + x – 6)
y’ = 0 => x = -3 hoặc x = 2
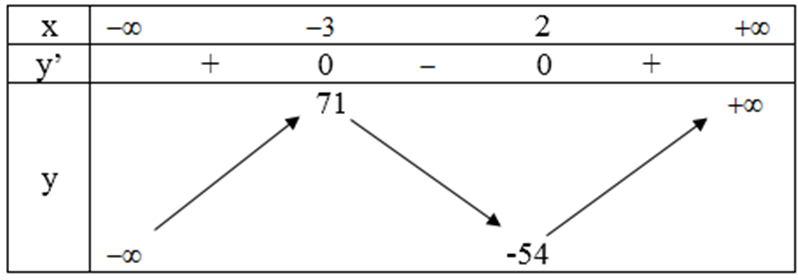
Bảng biến thiên:
Vậy đồ thị của hàm số có điểm cực đại là (-3; 71) và điểm cực tiểu là (2; -54).
b) TXĐ: D = R
y’= 4x3 + 4x = 4x(x2 + 1) = 0; y’ = 0 => x = 0
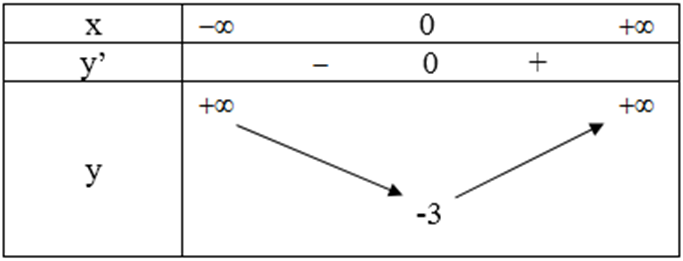
Bảng biến thiên:
Vậy hàm số có điểm cực tiểu là (0; -3).
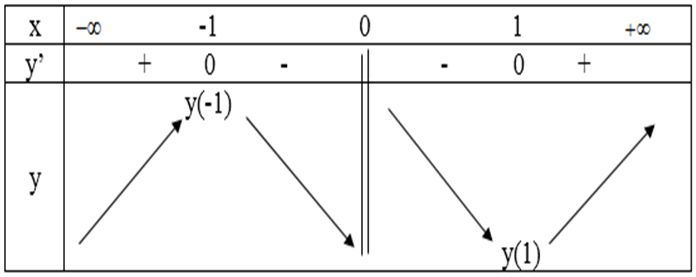
c) TXĐ: D = R \ {0}
y’ = 0 => x = ±1
Bảng biến thiên:
Vậy hàm số có điểm cực đại là xCĐ = -1 và điểm cực tiểu là xCT = 1.
d) TXĐ: D = R
Áp dụng công thức : (uv)’ = u’v + uv’.
Đạo hàm của hàm hợp: (un)’ = n.un – 1.u’
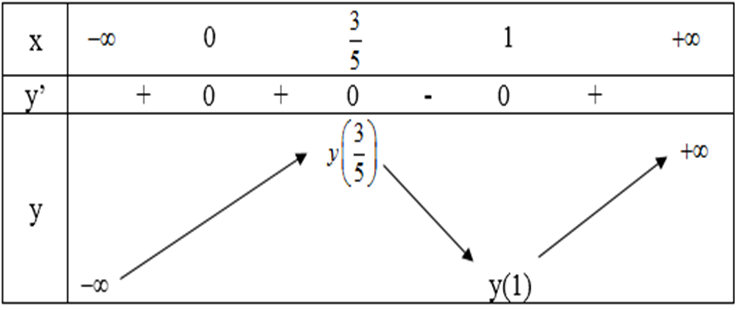
y’= 3x2(1 – x)2 – 2x3(1 – x) = x2(5x2 – 8x + 3)
y’ = 0 => x = 0; x = 1 hoặc x = 3/5
Bảng biến thiên:
Vậy hàm số cực đại xCĐ = 3/5 và điểm cực tiểu xCT = 1
(Lưu ý: x= 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)
e) Ta có:
Vậy D = R.
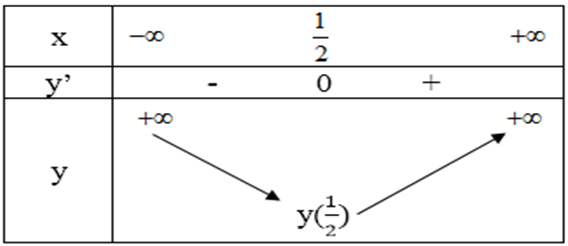
Bảng biến thiên:
Vậy hàm số có điểm cực tiểu xCT = 1/2.
Bài 2 (trang 18 SGK Giải tích 12): Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:
a) y = x4 – 2x2 + 1 ; b) y = sin2x – x
c) y = sinx + cosx ; d) y = x5 – x3 – 2x + 1
Lời giải:
a) TXĐ: D = R.
y’ = 4x3 – 4x
y’= 0 => x = 0; x = ±1.
y” = 12x2 – 4
y”(0) = -4 < 0 => x = 0 là điểm cực đại của hàm số.
y”(±1) = 8 > 0 > x = -1 và x = 1 là điểm cực tiểu của hàm số.
b) TXĐ: D = R
y’ = 2cos2x – 1;
c) TXĐ: D = R
d) TXĐ: D = R
y’= 5x4 – 3x2 – 2
y’ = 0 => x ±1.
y” = 20x3 – 6x
y”(-1) = -20 + 6 = -14 < 0 => x = -1 là điểm cực đại của hàm số.
y”(1) = 20 – 6 = 14 > 0 => x = 1 là điểm cực tiểu của hàm số.
Bài 3 (trang 18 SGK Giải tích 12): Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Lời giải:
Tính theo định nghĩa đạo hàm tại xo = 0 ta có:
Nghĩa là hàm số y = √|x| không có đạo hàm tại x = 0. (1)
Mặt khác ta có: √|x| ≥ 0 ∀ x. Dấu “=” xảy ra khi x = 0.
Do đó hàm số y = √|x| đạt cực tiểu tại x = 0. (2)
Từ (1) và (2) suy ra điều phải chứng minh.
Bài 4 (trang 18 SGK Giải tích 12): Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 – mx2 – 2x + 1
luôn luôn có một cực đại và một điểm cực tiểu.
Lời giải:
Xét hàm số y = x3 – mx2 – 2x + 1 ta có:
TXĐ: D = R
y’ = 3x2 – 2mx – 2
Với mọi giá trị của m ta đều có x1 < 0 < x2.
Bảng biến thiên:
Từ bảng trên ta thấy hàm số luôn có một điểm cực đại xCĐ = x1 và một điểm cực tiểu xCT = x2 với mọi giá trị của m (đpcm).
Bài 5 (trang 18 SGK Giải tích 12): Tìm a và b để các cực trị của hàm số
đều là nhưng số dương và xo = -5/9 là điểm cực đại.
Lời giải:
– Nếu a = 0 thì y = –9x + b. Vậy hàm số không có cực trị.
– Nếu a ≠ 0. Ta có: y’= 5a2x2 + 4ax – 9
y’= 0 => x = 1/a hoặc x = -9/5a
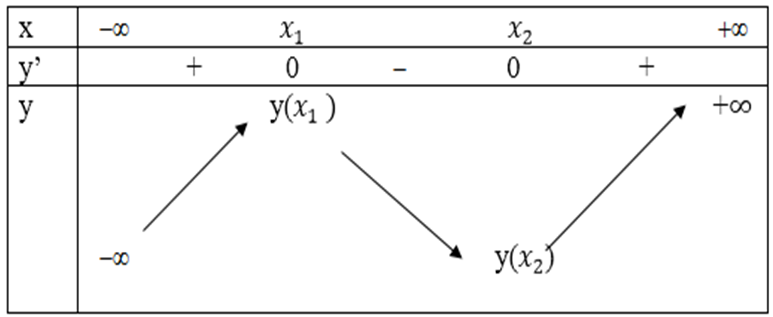
+ Với a > 0 ta có bảng biến thiên:
Vì xo = -5/9 là điểm cực đại nên
Theo đề bài thì yCT dương nên với a = 81/25 thì khi đó:
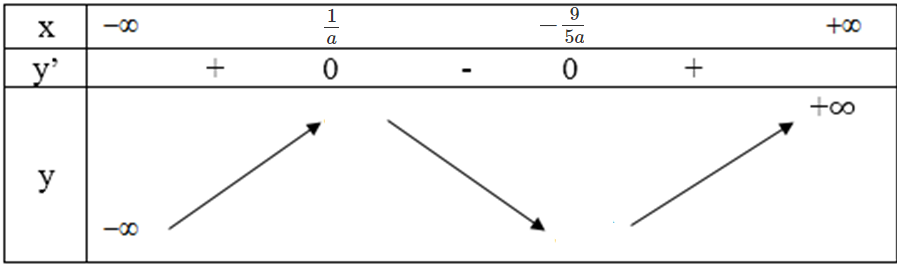
+ Với a < 0 ta có bảng biến thiên:
Vì xo = -5/9 là điểm cực đại nên
Theo đề bài thì yCT dương nên với a = -9/5 thì khi đó:
Vậy các giá trị a, b cần tìm là:
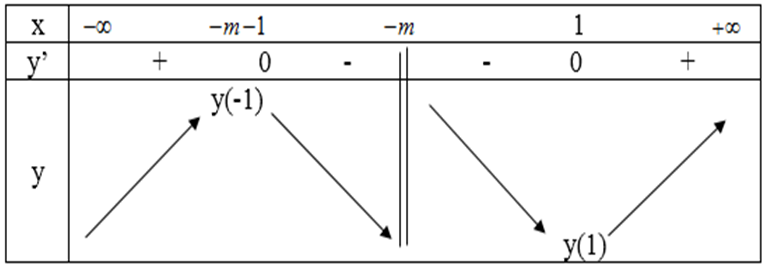
Bài 6 (trang 18 SGK Giải tích 12): Xác định giá trị của tham số m để hàm số m để hàm số
đạt giá trị cực đại tại x = 2.
Lời giải:
TXĐ: D = R \ {-m}
y’ = 0 => x1 = -m – 1; x2 = -m + 1
Bảng biến thiên:
Hàm số đạt cực đại tại x = 2 ⇔ – m – 1 = 2 => m = –3.