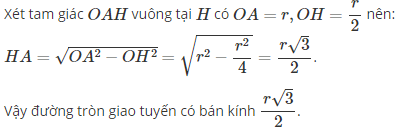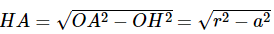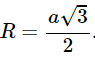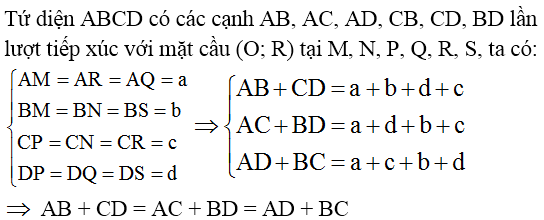Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 43: Tìm tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước.

Lời giải:

Tập hợp tâm các mặt cầu luôn luôn đi qua hai điểm cố định A và B cho trước là đường trung trực của đoạn thẳng AB

Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 45:

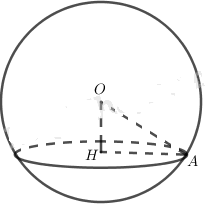
a) Hãy xác định đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng r/2.

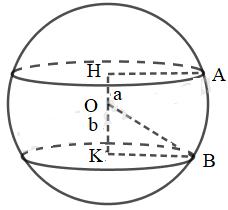
b) Cho mặt cầu S(O; r), hai mặt phẳng (α) và (β) có khoảng cách đến tâm O của mặt cầu đã cho lần lượt là a và b (0 < a < b < r). Hãy so sánh hai bán kính của các đường tròn giao tuyến.

Lời giải:

a)

Đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) là đường tròn tâm H có bán kính là:

b) áp dụng câu a bán kính các đường tròn giao tuyến là 

Vì 0 < a < b < r ⇒ 

Vậy đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) có bán kính lớn hơn mặt cầu S(O; r) và mặt phẳng (β)

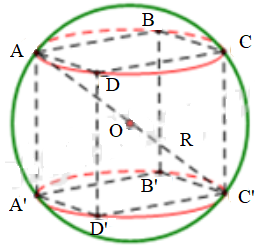
Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 48: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:

a) Đi qua 8 đỉnh của hình lập phương.

b) Tiếp xúc với 12 cạnh của hình lập phương.

c) Tiếp xúc với 6 mặt của hình lập phương.

Lời giải:

a) Tâm là giao điểm các đường chéo (O)

Bán kính mặt cầu là OA = 1/2 AC’

Đường chéo hình vuông cạnh a là a√2 (AC = a√2)

Xét tam giác vuông ACC’ tại C:

⇒ bán kính mặt cầu đi qua 8 đỉnh hình lập phương là (a√3)/2

b) không có mặt cầu tiếp xúc với 12 cạnh của hình lập phương

c)

Tâm mặt cầu tiếp xúc 6 mặt của hình lập phương là trung điểm O của EE’

Bán kính mặt cầu là OE = 1/2 EE’ = 1/2 AA’ = 1/2 a

Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 48: Cho hình lập phương ngoại tiếp mặt cầu bán kính r cho trước. Hãy tính thể tích của hình lập phương đó.

Lời giải:

Hình lập phương ngoại tiếp mặt cầu bán kính r có cạnh bằng 2r

Thể tích hình lập phương đó là: (2r)³ = 8r³

Bài 1 (trang 49 SGK Hình học 12): Tìm tập hợp tất cả các điểm M trong không gian luôn luôn nhìn một đoạn thẳng AB cố định dưới một góc vuông.

Lời giải:

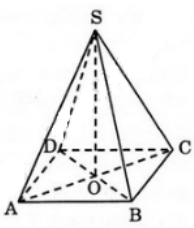
Bài 2 (trang 49 SGK Hình học 12): Cho hình chóp tứ giác đều S.ABCD có cạnh đều bằng a. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.

Lời giải:

Bài 3 (trang 49 SGK Hình học 12): Tìm tập hợp tâm các mặt cầu luôn chứa một đường tròn cố định cho trước.

Lời giải:

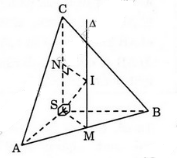
Bài 4 (trang 49 SGK Hình học 12): Tìm tập hợp tâm các mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.

Lời giải:

*Xét mặt cầu (S) có tâm O, bán kính R và tiếp xúc với ba cạnh BC, CA, AB của tam giác ABC tại M, N, P. H là hình chiếu vuông góc của O trên mp(ABC), ta có:

OM ⊥ AB => BM ⊥ AB

(theo định lí ba đường vuông góc)

Tương tự: HN ⊥ BC, HP ⊥ AC

Ta có: OM = ON = OP = R

Khi đó ΔOHM = ΔOHN = ΔOHP

Suy ra HM = HN = HP

Chứng tỏ H là tâm đường tròn nội tiếp tam giác ABC.

Vậy tâm O của mặt cầu thuộc đường thẳng d vuông góc với mp(ABC) tại tâm H của đường tròn nội tiếp tam giác ABC.

*Lấy điểm O thuộc trục đường tròn nội tiếp tam giác ABC.

Đường tròn nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại N, P, M, ta có: HM ⊥ AB, HN ⊥ BC, HP ⊥ CA

OM ⊥ AB, ON ⊥ BC, OP ⊥ CA (1)

Mặt khác: HM = HN = HP => ΔOHM = ΔOHN = ΔOHP

OM = ON = OP (2)

Từ (1) và (2) suy ra mặt cầu (S) tiếp xúc với ba cạnh của tam giác ABC. Vậy tập hợp tâm của các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là trục đường tròn nội tiếp tam giác ABC.

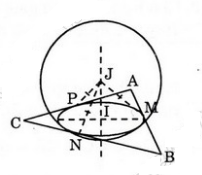
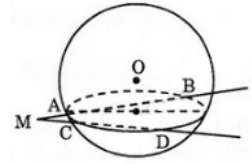
Bài 5 (trang 49 SGK Hình học 12): Từ một điểm M nằm ngoài mặt cầu (O; R), vẽ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.

a) Chứng minh rằng MA.MB = MC.MD

b) Gọi MO = d. Tính MA.MB theo R và d.

Lời giải:

a) Hai đường thẳng MAB và MCD giao nhau xác định một mặt phẳng (P). Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C), ngoại tiếp tứ giác phẳng ABCD.

Trong mặt phẳng (P) thì các tích MA.MB và MC.MD là giá trị của phương tích của điểm M đối với đường tròn (C), do đó:

MA.MB = MC.MD.

b) Mặt phẳng (OAB) cắt mặt cầu theo đường tròn lớn và phương tích của điểm M đối với đường tròn này là :

P_M/(O) = MA.MB = d² – R²(vì d > R).

Bài 6 (trang 49 SGK Hình học 12): Cho mặt cầu (O; R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc (AMB)= góc (AIB)

Lời giải:

Bài 7 (trang 49 SGK Hình học 12): Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA’ = a, AB = b, AD = c.

a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.

b) Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.

Lời giải:

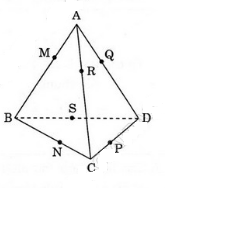
Bài 8 (trang 49 SGK Hình học 12): Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng các cặp cạnh đối diện của tứ diện bằng nhau.

Lời giải:

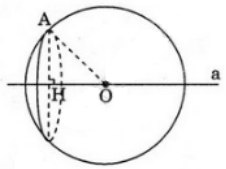
Bài 9 (trang 49 SGK Hình học 12): Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định

Lời giải:

Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.

Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.

Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

Bài 10 (trang 49 SGK Hình học 12): Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.

Lời giải: