- Giải bài tập SGK toán 6 Tập 1-Bài 2: Tập hợp các số tự nhiên
- Giải bài tập SGK toán 6 Tập 1-bài 3: Ghi số tự nhiên
- Giải bài tập SGK toán 6 Tập 1, Phần số Học- bài 4: Số phần tử của một tập hợp. Tập hợp con
- Giải bài tập SGK toán 6 Tập 1, Phần số Học- Luyện tập trang 14
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 5: Phép cộng và phép nhân
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1 + 2 (trang 17-18)
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Bài 6: Phép trừ và phép chia
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1 trang 24
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 2 trang 25
- Giải bài tập skg toán 6 Tập 1, Phần số Học-bài 7: Lũy thừa với số mũ tự nhiên. Nhân hai lũy thừa cùng cơ số
- Giải bài tập SGK bài tập toán 6 Tập 1, Phần số Học-Luyện tập trang 28
- Giải bài bài tập SGK tập toán 6 Tập 1, Phần số Học-bài 8: Chia hai lũy thừa cùng cơ số
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 9: Thứ tự thực hiện các phép tính
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 10: Tính chất chia hết của một tổng
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 36
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Giải toán 6 bài 11: Dấu hiệu chia hết cho 2, cho 5
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 39
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 12: Dấu hiệu chia hết cho 3, cho 9
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 42
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 13: Ước và bội
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 47
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Bài 15: Phân tích một số ra thừa số nguyên tố
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập (trang 50)
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 16: Ước chung và bội chung
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 53
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 17: Ước chung lớn nhất
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1+2 trang 56,57
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 18: Bội chung nhỏ nhất
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1 trang 59
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 2 trang 60
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Ôn tập chương 1 (trang 63-64)
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 1: Làm quen với số âm
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 2: Tập hợp các số nguyên
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 73
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 4: Cộng hai số nguyên cùng dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 5: Cộng hai số nguyên khác dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 77
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Bài 6: Tính chất của phép cộng các số nguyên
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 79
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 7: Phép trừ hai số nguyên
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 82
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 8: Quy tắc dấu ngoặc
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 9: Quy tắc chuyển vế
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 87
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 10: Nhân hai số nguyên khác dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 11: Nhân hai số nguyên cùng dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- Luyện tập trang 92
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- bài 12: Tính chất của phép nhân
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- Luyện tập trang 95
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- bài 13: Bội và ước của một số nguyên
- Giải bài tập SGK toán 6 tập 1 Chương II: Số Nguyên- Ôn tập chương 2
- Số Nguyên- Ôn tập chương 2
- Số Nguyên- bài 13: Bội và ước của một số nguyên
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 1: Điểm. Đường thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 2: Ba điểm thẳng hàng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 3: Đường thẳng đi qua hai điểm
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 5 : Tia
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 113
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 6: Đoạn thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 7: Độ dài đoạn thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-Bài 8: Khi nào thì AM + MB = AB?
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 9: Vẽ đoạn thẳng cho biết độ dài
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 10: Trung điểm của đoạn thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 10: Trung điểm của đoạn thẳng
1 (trang 61 sgk Toán 6 Tập 1): Viết dạng tổng quát các tính chất giao hoán, kết hợp của phép cộng, phép nhân, tính chất phân phối của phép nhân đối với phép cộng.
Trả lời:
| Phép tính | Cộng | Nhân |
| Giao hoán | a + b = b + a | a.b = b.a |
| Kết hợp | (a + b) + c = a + (b + c) | (a.b).c = a.(b.c) |
| Phân phối | a(b + c) = ab + ac | |
2 (trang 61 sgk Toán 6 Tập 1): Lũy thừa bậc n của a là gì?
Trả lời:
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an = a . a . .... . a (n ≠ 0)
n thừa số
3 (trang 61 sgk Toán 6 Tập 1): Viết công thức nhân hai lũy thừa cùng cơ số, chia hai lũy thừa cùng cơ số.
Trả lời:
– Nhân hai lũy thừa cùng cơ số:
am . an = am+n
– Chia hai lũy thừa cùng cơ số:
am : an = am-n (a ≠ 0; m ≥ n)
4 (trang 61 sgk Toán 6 Tập 1): Khi nào ta nói số tự nhiên a chia hết cho số tự nhiên b.
Trả lời:
Số tự nhiên a chia hết cho số tự nhiên b khác 0 nếu có số tự nhiên k sao cho a = b.k.
Kí hiệu: a ⋮ b
5 (trang 61 sgk Toán 6 Tập 1): Phát biểu và viết dạng tổng quát hai tính chất chia hết của một tổng.
Trả lời:
– Tính chất 1: a ⋮ m và b ⋮ m => (a + b) ⋮ m
Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
a ⋮ m, b ⋮ m và c ⋮ m => (a + b + c) ⋮ m
– Tính chất 2: a :/. m và b ⋮ m => (a + b) :/. m
Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
a :/. m, b ⋮ m và c ⋮ m => (a + b + c) :/. m
6 (trang 61 sgk Toán 6 Tập 1): Phát biểu các dấu hiệu chia hết cho 2, cho 3, cho 5, cho 9.
Trả lời:
– Dấu hiệu chia hết cho 2: Các số có chữ số tận cùng là chữ số chẵn thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
– Dấu hiệu chia hết cho 3: Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
– Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
– Dấu hiệu chia hết cho 9: Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
7 (trang 61 sgk Toán 6 Tập 1): Thế nào là số nguyên tố, hợp số ? Cho ví dụ.
Trả lời:
– Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Ví dụ: 2, 3, 5, 7, 11, …
– Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Ví dụ: 4, 6, 8, 9, …
8 (trang 61 sgk Toán 6 Tập 1): Thế nào là hai số nguyên tố cùng nhau ? Cho ví dụ.
Trả lời:
– Hai số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau.
Ví dụ: 8 và 9 là hai số nguyên tố cùng nhau.
9 (trang 61 sgk Toán 6 Tập 1): ƯCLN của hai hay nhiều số là gì ? Nêu cách tìm.
Trả lời:
– ƯCLN của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
– Cách tìm:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
10 (trang 61 sgk Toán 6 Tập 1): BCNN của hai hay nhiều số là gì ? Nêu cách tìm.
Trả lời:
– BCNN của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.
– Cách tìm:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Bài 159 (trang 63 sgk Toán 6 Tập 1): Tìm kết quả của các phép tính:
a) n – n ; b) n:n ; c) n + 0
d) n – 0 ; e) n.0 ; g) n.1 ; h) n:1
Lời giải:
a) n – n = 0 ; b) n:n = 1 ; c) n + 0 = n
d) n – 0 = n ; e) n.0 = 0 ; g) n.1 = n ;
h) n:1 = n
Có bạn nào có thắc mắc rằng n là gì không?. Ở đây n là một số tự nhiên nhé.
Bài 160 (trang 63 sgk Toán 6 Tập 1): Thực hiện các phép tính:
a) 204 – 84:12 ; b) 15.23 + 4.32 – 5.7
c) 56:53 + 23.22 ; d) 164.53 + 47.164
Lời giải:
Mục đích của bài này là kiểm tra kiến thức của các bạn về thứ tự thực hiện phép tính.
Lũy thừa –> Nhân và chia –> Cộng và trừ
a) 204 – 84:12 = 204 – 7 = 197
b) 15.23 + 4.32 – 5.7
= 15.8 + 4.9 – 5.7
= 120 + 36 – 35
= 121
c) Áp dụng:
am . an = am+n
am : an = am-n
56:53 + 23.22
= 53 + 25
= 125 + 32
= 157
d) Áp dụng tính chất phân phối của phép nhân đối với phép cộng để tính nhanh hơn.
164.53 + 47.164
= 164(53 + 47)
= 164.100
= 16400
Bài 161 (trang 63 sgk Toán 6 Tập 1): Tìm số tự nhiên x biết:
a) 219 – 7(x + 1) = 100 ; b) (3x – 6).3 = 34
Lời giải:
Áp dụng:
(Số bị trừ) - (Số trừ) = (Hiệu)
=> (Số trừ) = (Số bị trừ) - (Hiệu)
và
a.b = c
=> a = c:a
a) 219 – 7(x + 1) = 100
7(x + 1) = 219 – 100
7(x + 1) = 119
x + 1 = 119:7
x + 1 = 17
x = 17 – 1
x = 16
b) (3x – 6).3 = 34
3x – 6 = 34:3
3x – 6 = 33
3x – 6 = 27
3x = 27 + 6
3x = 33
x = 33:3
x = 11
Bài 162 (trang 63 sgk Toán 6 Tập 1): Để tìm số tự nhiên x biết rằng nếu lấy số đó trừ đi 3 rồi chia cho 8 thì được 12, ta có thể viết (x – 3):8 = 12 rồi tìm x, ta được x = 99.
Bằng cách làm trên, hãy tìm số tự nhiên x, biết rằng nếu nhân nó với 3 rồi trừ đi 8 sau đó chia cho 4 thì được 7.
Lời giải:
Bài toán trên trở thành tìm x để (3x – 8) : 4 = 7.
(3x – 8):4 = 7
3x – 8 = 7.4
3x – 8 = 28
3x = 28 + 8
3x = 36
x = 36:3
x = 12
Nếu bạn chưa hiểu, bạn có thể theo dõi tiếp phần dưới:
- nếu nó nhân với 3 => 3.x
- rồi trừ đi 8 => 3.x - 8
- sau đó chia cho 4 => (3x - 8) : 4
- thì được 7 => (3x - 8) : 4 = 7
Bài 163 (trang 63 sgk Toán 6 Tập 1): Đố. Điền các số 25, 18, 22, 33 vào chỗ trống và giải bài toán sau:
Lúc … giờ , người ta thắp một ngọn nến có chiều cao … cm. Đến … giờ cùng ngày, ngọn nến chỉ còn cao … cm. Trong một giờ, chiều cao của ngọn nến giảm bao nhiêu xentimet?
Lời giải:
– Vì số chỉ giờ trong ngày không vượt quá 24 và số chỉ giờ lúc đầu nhỏ hơn lúc sau nên ta có: Lúc 18 giờ; Đến 22 giờ
– Chiều cao ngọn nến lúc sau sẽ thấp hơn lúc ban đầu nên ta có: chiều cao 33 cm; còn cao 25 cm.
Vậy bài toán là: Lúc 18 giờ, người ta thắp một ngọn nến có chiều cao 33 cm. Đến 22 giờ cùng ngày, ngọn nến chỉ còn cao 25 cm. Trong một giờ, chiều cao của ngọn nến giảm bao nhiêu xentimet?
Thời gian nến cháy là 22 – 18 = 4 (giờ)
Chiều cao ngon nến giảm trong 4 giờ là 33 – 25 = 8 (cm)
Vậy trong 1 giờ, chiều cao ngọn nến giảm 8:4 = 2 (cm).
Đáp số: 2cm
Bài 164 (trang 63 sgk Toán 6 Tập 1): Thực hiện phép tính rồi phân tích kết quả thừa số nguyên tố:
a) (1000 + 1):11 ; b) 142 + 52 + 22
c) 29.31 + 144:122 ; d) 333:3 + 225:152
Lời giải:
Đây là một dạng bài toán kết hợp, các bạn cần nắm vững các kiến thức về:
– Thứ tự thực hiện phép tính: trong ngoặc trước –> lũy thừa –> nhân và chia –> cộng và trừ
– Cách phân tích một số ra thừa số nguyên tố
a) (1000 + 1):11 = 1001:11 = 91
Phân tích ra thừa số nguyên tố:
91 | 7
13 | 13
1 |
Vậy 91 = 7.13
b) 142 + 52 + 22 = 196 + 25 + 4 = 225
Phân tích ra thừa số nguyên tố:
225 | 3
75 | 3
25 | 5
5 | 5
1 |
Vậy 255 = 32.52
c) 29.31 + 144:122 = 29.31 + 144:144 = 899 + 1 = 900
Phân tích ra thừa số nguyên tố:
900 | 2
450 | 2
225 | 3
75 | 3
25 | 5
5 | 5
1 |
Vậy 900 = 22.32.52
d) 333:3 + 225:152 = 111 + 225:225 = 111 + 1 = 112
Phân tích ra thừa số nguyên tố:
112 | 2
56 | 2
28 | 2
14 | 2
7 | 7
1 |
Vậy 112 = 24.7
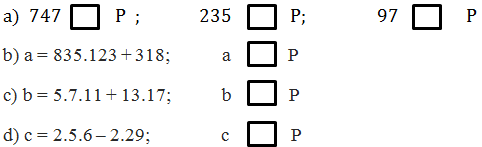
Bài 165 (trang 63 sgk Toán 6 Tập 1): Gọi P là tập hợp các số nguyên tố. Điền kí hiệu ∈ hoặc ∉ thích hợp vào ô vuông:
Lời giải:
a) 747 ∉ P ; 235 ∉ P ; 97 ∈ P
Giải thích:
747 có tổng 7 + 4 + 7 = 18 chia hết cho 3 và 9 nên 747 là hợp số.
235 có tận cùng là 5 nên chia hết cho 5 nên 235 là hợp số.
97 là số nguyên tố.
b) a ∉ P
Giải thích: Áp dụng tính chất chia hết của một tổng
a = 835.123 + 318 có:
– Thừa số 123 có tổng 1 + 2 + 3 = 6 chia hết cho 3 nên 835.123 chia hết cho 3.
– 318 có tổng 3 + 1 + 8 = 12 chia hết cho 3 nên 318 chia hết cho 3.
Do đó a = 835.123 + 318 chia hết cho 3 nên a là hợp số.
c) b ∉ P
Giải thích: Hai tích 5.7.11 và 13.17 là hai số lẻ nên tổng của chúng là số chẵn. Do đó b chia hết cho 2 nên b là hợp số.
d) c ∉ P
Giải thích: Hai tích 2.5.6 và 2.29 đều là số chẵn (vì cùng là bội của 2) nên hiệu của chúng cũng là số chẵn. Do đó c chia hết cho 2 nên c là hợp số.
Bài 166 (trang 63 sgk Toán 6 Tập 1): Viết các tập hợp sau bằng cách liệt kê các phần tử:
A = {x ∈ N | 84 ⋮ x, 180 ⋮ x và x > 6}
B = {x ∈ N | x ⋮ 12, x ⋮ 15, x ⋮ 18 và 0 < x < 300}
Lời giải:
a)
– Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180).
– Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180)
+ Phân tích: 84 = 22.3.7 ; 180 = 22.32.5
+ Các thừa số chung là 2, và 3
+ Số mũ nhỏ nhất của 2 là 2, của 3 là 1.
Do đó ƯCLN(84, 180) = 22.3 = 12
Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12}
– Vì x > 6 nên x = 12
Vậy A = {12}
b)
– Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18).
– Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18)
+ Phân tích: 12 = 22.3 ; 15 = 3.5 ; 18 = 2.32
+ Chọn thừa số chung, riêng: đó là 2, 3, 5
+ Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1.
Do đó BCNN(12, 15, 18) = 22.32.5 = 180
Suy ra BC(12, 15, 18) = {0, 180, 360, 540, …}
– Vì 0 < x < 300 nên x = 180
Vậy B = {180}
Bài 167 (trang 63 sgk Toán 6 Tập 1): Một số sách nếu xếp thành từng bó 10 quyển, 12 quyển hoặc 15 quyển đều vừa đủ bó. Tính số sách đó biết rằng số sách trong khoảng từ 100 đến 150.
Lời giải:
Vì nếu xếp số sách thành từng bó 10 quyển, 12 quyển hoặc 15 quyển đều vừa đủ nên số sách là một số chia hết cho cả 10, 12 và 15. Hay nói cách khác, số sách là BC(10, 12, 15).
Tìm BC(10, 12, 15) thông qua BCNN(10, 12, 15):
– Phân tích: 10 = 2.5 ; 12 = 22.3 ; 15 = 3.5
– Chọn thừa số chung, riêng: đó là 2, 3, 5
– Số mũ lớn nhất của 2 là 2, của 3 và 5 là 1
=> BCNN(10, 12, 15) = 22.3.5 = 60
Do đó BC(10, 12, 15) = {0, 60, 120, 180, …}
Theo đề bài, số sách trong khoảng từ 100 đến 150 (tức là 100 < số sách < 150) nên số sách = 120 (quyển).
Bài 167 (trang 63 sgk Toán 6 Tập 1): Một số sách nếu xếp thành từng bó 10 quyển, 12 quyển hoặc 15 quyển đều vừa đủ bó. Tính số sách đó biết rằng số sách trong khoảng từ 100 đến 150.
Lời giải:
Vì nếu xếp số sách thành từng bó 10 quyển, 12 quyển hoặc 15 quyển đều vừa đủ nên số sách là một số chia hết cho cả 10, 12 và 15. Hay nói cách khác, số sách là BC(10, 12, 15).
Tìm BC(10, 12, 15) thông qua BCNN(10, 12, 15):
– Phân tích: 10 = 2.5 ; 12 = 22.3 ; 15 = 3.5
– Chọn thừa số chung, riêng: đó là 2, 3, 5
– Số mũ lớn nhất của 2 là 2, của 3 và 5 là 1
=> BCNN(10, 12, 15) = 22.3.5 = 60
Do đó BC(10, 12, 15) = {0, 60, 120, 180, …}
Theo đề bài, số sách trong khoảng từ 100 đến 150 (tức là 100 < số sách < 150) nên số sách = 120 (quyển).
Bài 168 (trang 64 sgk Toán 6 Tập 1): Máy bay trực thăng ra đời năm nào?
Máy bay trực thăng ra đời năm abcd.
Biết rằng: a không là số nguyên tố, cũng không là hợp số;
b là số dư trong phép chia 105 cho 12;
c là số nguyên tố lẻ nhỏ nhất;
d là trung bình cộng của b và c.
Hình 29
Lời giải:
Theo bài ra, a không là số nguyên tố cũng không là hợp số nên suy ra a = 1 (a là số ở hàng nghìn nên a khác 0).
– 105:12 = 8 dư 9 nên b = 9.
– Số nguyên tố lẻ nhỏ nhất là 3 nên c = 3.
– Trung bình cộng của b và c là: (9 + 3):2 = 6 nên d = 6.
Vậy abcd = 1936 hay máy bay ra đời vào năm 1936.
Bài 169 (trang 64 sgk Toán 6 Tập 1): Đố:
Bé kia chăn vịt khác thường
Buộc đi cho được chẵn hàng mới ưa.
Hàng 2 xếp thấy chưa vừa,
Hàng 3 xếp vẫn còn thừa 1 con,
Hàng 4 xếp cũng chưa tròn,
Hàng 5 xếp thiếu 1 con mới đầy.
Xếp thành hàng 7, đẹp thay!
Vịt bao nhiêu? Tính được ngay mới tài!
(Biết số vịt chưa đến 200 con)
Lời giải:
Giải thích từ ngữ:
Hàng 2, Hàng 3, …: nghĩa là mỗi hàng có 2, 3, … con vịt.
chưa vừa, chưa tròn: nghĩa là còn dư
đẹp thay : nghĩa là đã xếp tròn hàng
– Số vịt chia cho 5 (xếp thành hàng 5) thì thiếu 1 con nên số vịt là số tận cùng bằng 4 hoặc 9.
– Mà khi xếp hàng 2 thì còn dư nên số vịt có chữ số tận cùng bằng 9.
– Khi xếp hàng 7 thì vừa tròn nên số vịt là một số chia hết cho 7 (hay là bội số của 7).
Vì có số tận cùng bằng 9 nên số vịt có thể bằng 49, 119, 189, …
– Số vịt chia cho 3 dư 1 (khi xếp hàng 3 thì dư 1 con) và số vịt < 200 nên số vịt = 119 (con).
Đáp số: 119 con