- Giải bài tập SGK toán 6 Tập 1-Bài 2: Tập hợp các số tự nhiên
- Giải bài tập SGK toán 6 Tập 1-bài 3: Ghi số tự nhiên
- Giải bài tập SGK toán 6 Tập 1, Phần số Học- bài 4: Số phần tử của một tập hợp. Tập hợp con
- Giải bài tập SGK toán 6 Tập 1, Phần số Học- Luyện tập trang 14
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 5: Phép cộng và phép nhân
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1 + 2 (trang 17-18)
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Bài 6: Phép trừ và phép chia
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1 trang 24
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 2 trang 25
- Giải bài tập skg toán 6 Tập 1, Phần số Học-bài 7: Lũy thừa với số mũ tự nhiên. Nhân hai lũy thừa cùng cơ số
- Giải bài tập SGK bài tập toán 6 Tập 1, Phần số Học-Luyện tập trang 28
- Giải bài bài tập SGK tập toán 6 Tập 1, Phần số Học-bài 8: Chia hai lũy thừa cùng cơ số
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 9: Thứ tự thực hiện các phép tính
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 10: Tính chất chia hết của một tổng
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 36
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Giải toán 6 bài 11: Dấu hiệu chia hết cho 2, cho 5
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 39
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 12: Dấu hiệu chia hết cho 3, cho 9
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 42
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 13: Ước và bội
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 47
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Bài 15: Phân tích một số ra thừa số nguyên tố
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập (trang 50)
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 16: Ước chung và bội chung
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập trang 53
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 17: Ước chung lớn nhất
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1+2 trang 56,57
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-bài 18: Bội chung nhỏ nhất
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 1 trang 59
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Luyện tập 2 trang 60
- Giải bài tập SGK toán 6 Tập 1, Phần số Học-Ôn tập chương 1 (trang 63-64)
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 1: Làm quen với số âm
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 2: Tập hợp các số nguyên
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 73
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 4: Cộng hai số nguyên cùng dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 5: Cộng hai số nguyên khác dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 77
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Bài 6: Tính chất của phép cộng các số nguyên
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 79
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 7: Phép trừ hai số nguyên
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 82
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 8: Quy tắc dấu ngoặc
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 9: Quy tắc chuyển vế
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-Luyện tập trang 87
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 10: Nhân hai số nguyên khác dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên-bài 11: Nhân hai số nguyên cùng dấu
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- Luyện tập trang 92
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- bài 12: Tính chất của phép nhân
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- Luyện tập trang 95
- Giải bài tập SGK toán 6 Chương II: Số Nguyên- bài 13: Bội và ước của một số nguyên
- Giải bài tập SGK toán 6 tập 1 Chương II: Số Nguyên- Ôn tập chương 2
- Số Nguyên- Ôn tập chương 2
- Số Nguyên- bài 13: Bội và ước của một số nguyên
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 1: Điểm. Đường thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 2: Ba điểm thẳng hàng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 3: Đường thẳng đi qua hai điểm
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 5 : Tia
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-Luyện tập trang 113
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 6: Đoạn thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 7: Độ dài đoạn thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-Bài 8: Khi nào thì AM + MB = AB?
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 9: Vẽ đoạn thẳng cho biết độ dài
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 10: Trung điểm của đoạn thẳng
- Giải bài tập SGK toán 6 tập 1 Phần Hình Học – Chương 1-bài 10: Trung điểm của đoạn thẳng
Quy tắc: Muốn nhân hai số nguyên âm, ta nhân hai giá trị tuyệt đối của chúng.
(Số âm) . (Số âm) = (Số dương)
Nhận biết dấu của tích:
(+) . (+) –> (+)
(-) . (-) –> (+)
(+) . (-) –> (-)
(-) . (+) –> (-)
Hay nói ngắn gọn:
- Tích hai số cùng dấu thì dương.
- Tích hai số khác dấu thì âm.
Trả lời câu hỏi Toán 6 Tập 1 Bài 11 trang 90: Tính
a) 12 . 3;
b) 5 . 120.
Lời giải
a) 12 . 3 = 36
b) 5 . 120 = 600
Trả lời câu hỏi Toán 6 Tập 1 Bài 11 trang 90: Hãy quan sát kết quả bốn tích đầu và dự đoán kết quả của hai
3.(-4) = -12
tăng 4
2.(-4) = -8
tăng 4
1.(-4) = -4
tăng 4
0.(-4) = 0
(-1).(-4) = ?
(-2).(-4) = ?
Lời giải
Ta có: (-1) . (-4) = 4
(-2) . (-4) = 8
Trả lời câu hỏi Toán 6 Tập 1 Bài 11 trang 90: Tính:
a) 5 . 17;
b) (-15) . (-6).
Lời giải
Ta có:
a) 5 . 17 = 85
b) (-15) . (-6) = 90
Trả lời câu hỏi Toán 6 Tập 1 Bài 11 trang 91: Cho a là một số nguyên dương. Hỏi b là số nguyên dương hay nguyên âm nếu:
a) Tích a . b là một số nguyên dương ?
b) Tích a . b là một số nguyên âm ?
Lời giải
a) a là một số nguyên dương. Tích a . b là một số nguyên dương
Suy ra b là một số nguyên dương
b) a là một số nguyên dương. Tích a . b là một số nguyên âm
Suy ra b là một số nguyên âm
Bài 78: Tính:
a) (+3).(+9) b) (-3).7 c) 13.(-5) d) (-150).(-4) e) (+7).(-5)Lời giải
Quy tắc: Muốn nhân hai số nguyên âm, ta nhân hai giá trị tuyệt đối của chúng.
(Số âm) . (Số âm) = (Số dương)
Các phần b, c, e là nhân hai số nguyên khác dấu. Hai phần a và d là nhân hai số nguyên cùng dấu.
a) (+3).(+9) = 27 b) (-3).7 = -(3.7) = -21 c) 13.(-5) = -(13.5) = -65 d) (-150).(-4) = 150.4 = 600 e) (+7).(-5) = -(7.5) = -35
Bài 79: Tính 27.(-5). Từ đó suy ra các kết quả:
(+27).(+5); (-27).(+5); (-27).(-5); (+5).(-27)
Lời giải
Nhận biết dấu của tích:
(+) . (+) –> (+)
(-) . (-) –> (+)
(+) . (-) –> (-)
(-) . (+) –> (-)
Ta có: 27.(-5) = -(27.5) = -135
Suy ra:
(+27).(+5) = 135
(-27).(+5) = -135
(-27).(-5) = 135
(+5).(-27) = -135
Bài 80: Cho a là một số nguyên âm. Hỏi b là số nguyên âm hay số nguyên dương nếu biết:
a) a.b là một số nguyên dương?
b) a.b là một số nguyên âm?
Lời giải
Nhận biết dấu của tích:
(+) . (+) –> (+)
(-) . (-) –> (+)
(+) . (-) –> (-)
(-) . (+) –> (-)
Hay nói ngắn gọn:
- Tích hai số cùng dấu thì dương.
- Tích hai số khác dấu thì âm.
a) Vì tích hai số là nguyên dương nên hai số là cùng dấu. Mà a là số nguyên âm nên suy ra b cũng là số nguyên âm.
b) Vì tích hai số là nguyên âm nên hai số là khác dấu. Mà a là số nguyên âm nên suy ra b là số nguyên dương.
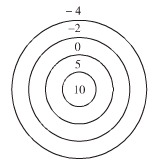
Bài 81: Trong trò chơi bắn bi vào các hình tròn vẽ trên mặt đất (h.52), bạn Sơn bắn được ba viên điểm 5, một viên điểm 0 và hai viên điểm -2; bạn Dũng bắn được hai viên điểm 10, một viên điểm -2 và ba viên điểm -4. Hỏi bạn nào được điểm cao hơn?
Hình 52
Lời giải
Tổng số điểm của bạn Sơn bắn được là:
3.5 + 1.0 + 2.(-2) = 15 – 4 = 11 điểm
Tổng số điểm của bạn Dũng bắn được là:
2.10 + 1.(-2) + 3.(-4) = 20 – 2 – 12 = 6 điểm
Bài 82: So sánh:
a) (-7).(-5) với 0; b) (-17).5 với (-5).(-2)
c) (+19).(+6) với (-17).(-10)
Lời giải
Các bạn có thể tính toán ra kết quả rồi so sánh hoặc áp dụng:
- Tích hai số cùng dấu thì dương.
- Tích hai số khác dấu thì âm.
a) Tích gồm hai số nguyên cùng dấu nên kết quả là số dương.
Do đó: (-7).(-5) > 0
hoặc: (-7).(-5) = 35 > 0
b) (-17).5 là tích của hai số nguyên khác dấu nên < 0
(-5).(-2) là tích của hai số nguyên cùng dấu nên > 0
Do đó: (-17).5 < (-5).(-2)
hoặc: (-17).5 = -85; (-5).(-2) = 10
Vì -85 < 10 nên (-17).5 < (-5).(-2)
c) (+19).(+6) với (-17).(-10)
(+19).(+6) = 114; (-17).(-10) = 170