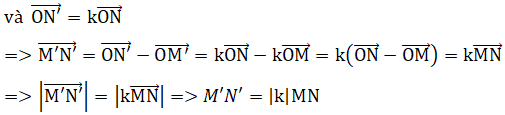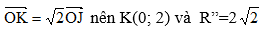Để xem lời giải chi tiết SGK lớp 3,4,5,6,7,8,9,10,11,12 vui lòng truy cập website : edusmart.vn

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 30: Chứng minh nhận xét 2.

Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

Lời giải

Phép vị tự tâm O, tỉ số k biến điểm M, N thành 2 điểm M’,N’ sao cho OM’→ = kOM→

Vậy phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 30: Chứng minh nhận xét 3.

Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk.

Lời giải

– Phép đồng dạng tỉ số k biến 2 điểm M, N thành 2 điểm M’,N’ sao cho M’N’ = kMN

– Phép đồng dạng tỉ số b biến 2 điểm M’,N’ thành 2 điểm M”,N”sao cho M”N” = pM’N’

⇒ M”N” = pkMN

Vậy: Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 31: Chứng minh tính chất a.

Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

Lời giải

Phép đồng dạng tỉ số k biến 3 điểm A, B, C thẳng hàng thành 3 điểm A’,B’,C’ sao cho:

A’B’ = kAB, B’C’ = kBC, A’C’ = kAC

A, B, C thẳng hàng và B nằm giữa A, C ⇔ AB + BC = AC

Do đó kAB + kBC = kAC hay A’B’ + B’C’ = A’C’

⇒ A’, B’, C’ thẳng hàng và B’ nằm giữa A’, C’

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 31: Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.

Lời giải

A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB

M’ = F(M) ⇒ A’M’ = kAM

M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’

Vậy M’ là trung điểm của A’B’

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 33: Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau không?

Lời giải

Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau

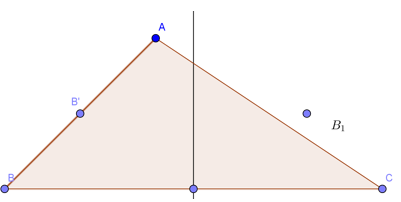
Bài 1 (trang 33 SGK Hình học 11): Cho tam giác ABC. Dựng ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B có tỉ số ½ và phép đối xứng qua đường trung trực của BC.

Lời giải:

• Qua phép vị tự ∂_{(B; 1/2)}

*A biến thành B’, B’ là trung điểm của BA vì BB’= ½BA

*B biến thành chính nó.

*C biến thành C’, C’ là trung điểm của BC vì BC’= ½BC

• Qua phép đối xứng trục ĐΔ ( Δ là trung trực của BC).

*B’ biến thành B1 (Δ là đường thẳng trung trực của B’B1)

*B biến thành C.

*C’ biến thành chính nó.

Vậy thực hiện liên tiếp phép vị tự và phép đối xứng trục ĐΔ, tam giác ABC biến thành tam giác B1CC’.

Bài 2 (trang 33 SGK Hình học 11): Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L, J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh rằng hai hình thang JLKI và IHDC đồng dạng với nhau.

Lời giải:

Trước hết thực hiện phép đối xứng tâm I, ta có:

C → A, D → B, H → K.

Hình thanh IHDC → hình thang IKBA.

Tiếp theo thực hiện phép vị tự tâm C, tỉ số k = 1/2 , ta có:

A → I, I → J, B → K, K → L

Hình thang IKBA → hình thang JLKI.

Vậy nếu thực hiện liên tiếp phép đối xứng Đ_I và phép vị tự V_(C;1/2) thì hình thang IHDC biến thành hình thang JLKI.

Suy ra hai hình thang IHDC và JLKI đồng dạng với nhau.

Bài 3 (trang 33 SGK Hình học 11): Trong mặt phẳng Oxy cho điểm I(1; 1) và đường tròn tâm I bán kính 2. Viết phương trình đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc 45^o và phép vị tự tâm O, tỉ số căn 2 .

Lời giải:

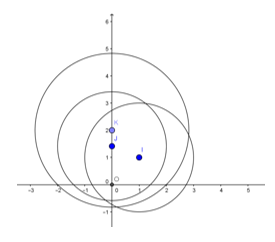
*I(1; 1) là đỉnh hình vuông có đường chéo OI = căn 2 nên OI với tia Oy góc 45^o. Q_{(O; 45^o)}, biến đường tròn tâm I(1; 1), bán kính R = 2 thành đường tròn tâm J_{(0; căn 2 )} và có cùng bán kính R’ = 2.

*V_{(O; căn 2)} , biến đường tròn tâm J bán kính R’ = 2 thành đường tròn tâm K bán kính R” thì

Vậy ảnh của đường tròn tâm I qua phép đồng dạng là đường tròn tâm K có phương trình x² + ( y – 2 )² = 8.

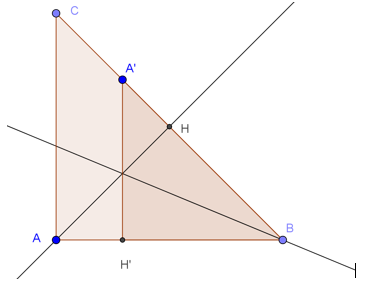
Bài 4 (trang 33 SGK Hình học 11): Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A, tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.

Lời giải:

Gọi d là đường phân giác của góc B của tam giác ABC.

Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC và biến B thành B do đó biến tam giác vuông HBA thành tam giác vuông H’BA’ bằng với nó.

Ta có H’A’ // AC, thực hiện tiếp theo phép vị tự tâm B, tỉ số

thì tam giác vuông H’BA’ biến thành tam giác vuông ABC.