Đề kiểm tra 1 tiết Toán 7 Chương 3 Hình học (Trắc nghiệm – Tự luận 1)

Đề kiểm tra Học kì 2 – Năm học ….

Môn Toán 7 – Đại Số

Thời gian làm bài: 45 phút

A. Phần trắc nghiệm (3 điểm)

Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:

Câu 1: Bộ ba số nào sau đây không thể là độ dài ba cạnh của một tam giác?

A. 1cm, 2cm, 2cm      B. 6cm, 7cm, 13cm

C. 3cm, 4cm, 6cm      D. 6cm, 7cm, 12cm

Câu 2: Tam giác ABC có độ dài hai cạnh là BC = 1cm, AC = 8cm. Tìm AB biết độ dài cạnh AB là một số nguyên.

A. 6cm      B. 7cm      C. 8cm      D. 9cm

Câu 3: Cho hình 1, quan hệ nào sau đây là đúng,

A. AC > AB > BC      B. AB > AC > BC

C. AC < BC < AB      D. AC > BC > AB

Câu 4: Giao điểm của ba đường cao trong tam giác được gọi là:

A. Trọng tâm của tam giác

B. Trực tâm của tam giác

C. Tâm đường tròn ngoại tiếp

D. Tâm đường tròn nội tiếp

Câu 5: Nếu AM là đường trung tuyến và G là trọng tâm tam giác ABC thì:

A. AM = AB           B. AG = 2/3 AM

C. AG = 3/4 AB           D. AM = AG

Câu 6: Cho tam giác ABC có ∠B = 45^o, ∠C = 75^o. Tía AD là tia phân giác của góc (BAC) (D ∈ BC). Khi đó số đo của góc (ADB) là:

A. 105^o      B. 100^o      C. 115^o      D. 120^o

B. Phần tự luận (7 điểm)

Câu 1: (2 điểm) Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.

a. Tính độ dài cạnh BC

b. So sánh các góc của tam giác ABC

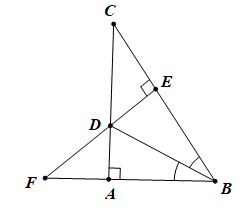
Câu 2: (5 điểm) Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:

a. ∆ABD = ∆EBD

b. BD là đường trung trực của AE

c. DF = DC

b. AD < DC

Đáp án và thang điểm

A. Phần trắc nghiệm (3 điểm)

Mỗi câu trả lời đúng được 0.5 điểm

1	2	3	4	5	6
B	C	D	B	B	A

Câu 1: Ta có: 6 + 7 = 13 không thỏa mãn bất đẳng thức tam giác nên chọn B

Câu 2: Ta có AC – BC < AB < AC + BC ⇒ 7 < AB < 9 ⇒ AB = 8cm.

Chọn C

Câu 3: Nhìn hình vẽ ta có ∠A = 180^o – 61^o – 59^o = 60^o.

Khi đó ∠C < ∠A < ∠B ⇒ AB < BC < AC hay AC > BC > AB. Chọn D

Câu 4: Chọn B

Câu 5: Chọn B

Câu 6: Ta có ∠A = 180^o – 45^o – 75^o = 60^o. Vì AD là tia phân giác nên

∠(BAD) = 30^o

Trong tam giác ADB có ∠(ADB) = 180^o – 45^o – 30^o = 105^o. Chọn A

B. Phần tự luận (7 điểm)

Câu 1

a. Áp dụng định lí Pytago trong tam giác ABC ta có:

BC² = AB² + AC² = 6² + 8² = 100 ⇒ BC = 10cm

b. Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A (quan hệ giữa góc và cạnh đối diện trong tam giác)

Câu 2

a. Hình vẽ (0.5 điểm)

Xét ∆ABD và ∆EBD có:

∠(ABD) = ∠(DBE)

BD là cạnh chung

⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)

b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)

Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AE

Vậy BD là đường trung trực của AE (0.5 điểm)

c. Xét ∆ADF và ∆EDC có:

AD = DE

∠(ADF) = ∠(EDC) (hai góc đối đỉnh)

⇒ ∆ADF = ∆EDC ( cạnh góc vuông – góc nhọn kề)(1 điểm)

⇒ DF = DC (hai cạnh tương ứng) (0.5 điểm)

d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất

⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)