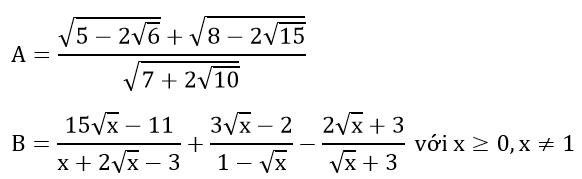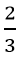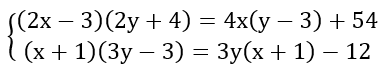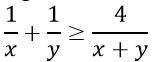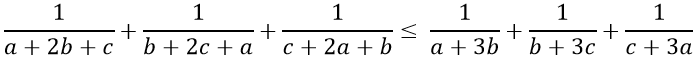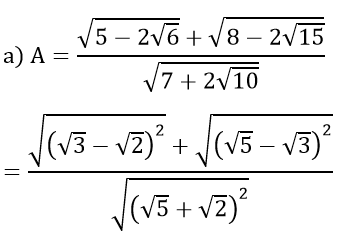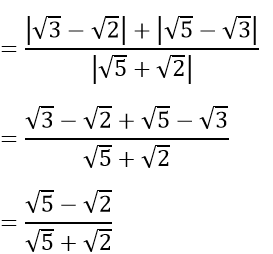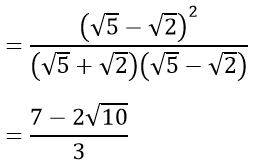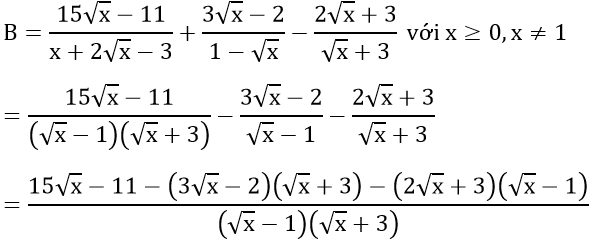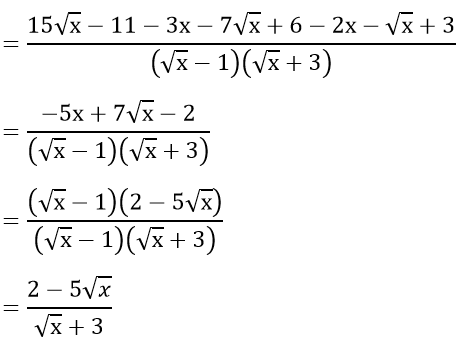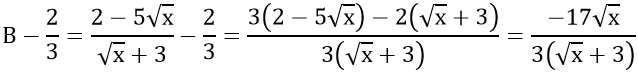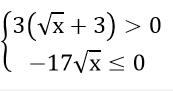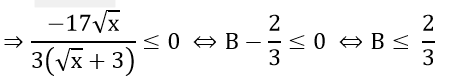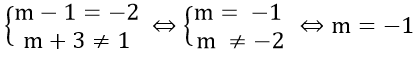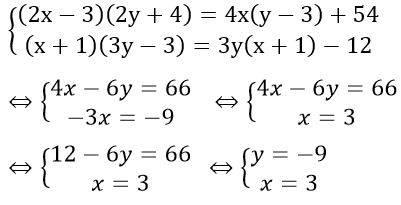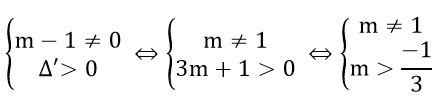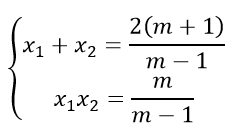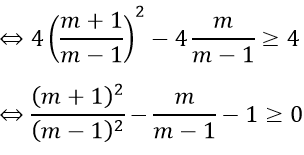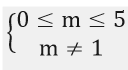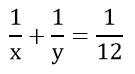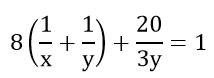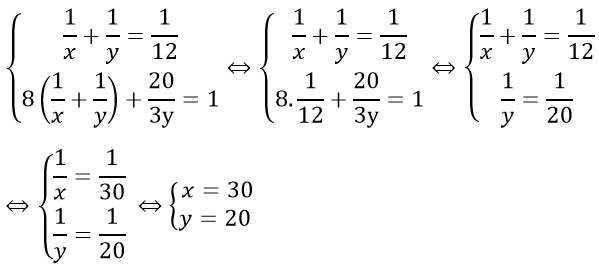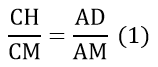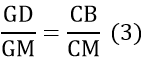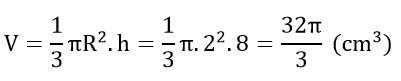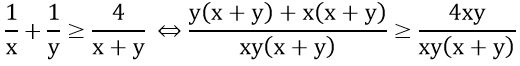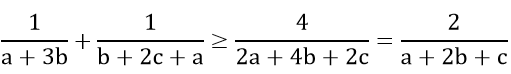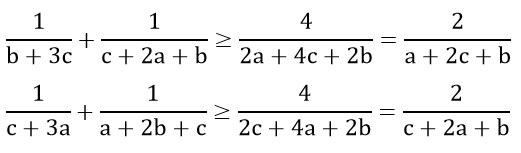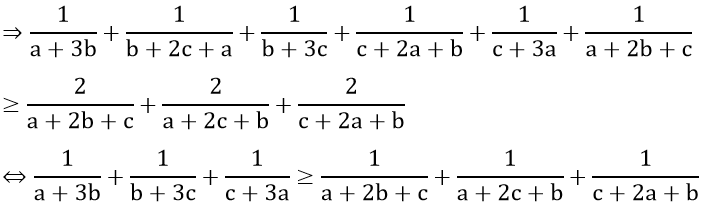- Tuyển tập 60 đề thi vào 10 các sở giáo dục có đáp án chi tiết
- Tuyển tập đề thi vào 10 năm học 2017-2018
- Đề thi môn Toán vào 10 (có đáp án – Đề 1)
- Đề thi môn Toán vào 10 (có đáp án – Đề 2)
- Đề thi môn Toán vào 10 (có đáp án – Đề 3)
- Đề thi môn Toán vào 10 (có đáp án – Đề 4)
- Đề thi môn Toán vào 10 (có đáp án – Đề 5)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 1)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 2)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 3)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 4)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 5)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 6)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 7)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 8)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 9)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 10)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 1)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 2)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 3)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 4)
- Đề thi thử vào 10 THPT thăng long lần 2 năm 2019
- TUYỂN TẬP ĐỀ THI VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2017-2018
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Lê Quý Đôn Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở gd và đt Vĩnh Phúc
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Tiền Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Thừa Thiên Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Thanh Hóa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Phú Thọ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Ninh Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Nam Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Long An
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Lạng Sơn
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hải Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hà Nội Chuyên Tin
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hà Nam
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đồng Nai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đà Nẵng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Thành Phố Cần Thơ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bình Phước
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt An Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bến Tre
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 Trường Thpt Chuyên Lê Quý Đôn Bình Định Chuyên Toán
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Chuyên Vĩnh Phúc
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Vĩnh Long
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Quảng Ngãi
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Lâm Đồng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Lai Châu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đồng Tháp
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Lương Thế Vinh Đồng Nai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên An Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Bà Rịa Vùng Tàu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Lạc Thủy Hòa Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên quốc học Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Quốc Học Huế Chuyên Toán
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Quốc Học Huế chuyên tin
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Lam Sơn Thanh Hóa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên KHTN Hà Nội vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên KHTN Hà Nội Vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Hùng Vương Phú Thọ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Hùng Vương Phú Thọ chuyên tin
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên đh Sư Phạm vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên đh Sư Phạm Hà Nội Vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Thực Hành Cao Nguyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Tây Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 Phòng Gd và Đt Giao Thủy
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Sơn Tây Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Nhân Chính Thanh Xuân
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường Thpt Phan Huy Chú Đống Đa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường Thcs Thái Thịnh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 cụm trường Thcs Quận Hai Bà Trưng
- Đề thi thử vào lớp 10 môn toán năm học 2017-2018 trường THCS ARCHIMEDES ACADEMY lần 6
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Lương Thế Vinh Hồ Chí Minh
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs An Đà Hải Phòng Lần 1
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở gd và đt Tam Đảo
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường Thpt Thăng Long Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Đào Duy Từ Thanh Hóa
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Võ Thị Sáu Hải Phòng
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Thiệu Vận Thanh Hóa Lần 1
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Nga Thiện Thanh Hóa
- Đề thi thử toán 9 năm 2018 trường thpt Chuyên khtn Hà Nội vòng 1 đợt 1
- Đề thi khảo sát toán 9 năm học 2017- 2018 phòng gd và đt Ba Đình Hà Nội
- Đề kscl Toán 9 năm học 2017-2018 phòng gd và đt Vĩnh Tường Vĩnh Phúc
- Đề kscl toán 9 năm học 2017-2018 phòng gd và đt Thanh Trì Hà Nội Lần 2
- Đề kscl toán 9 năm học 2017-2018 trường thcs Lê Quý Đôn Hà Nội Lần 2
- Đề kiểm tra giữa học kì 2 toán 9 toán 9 năm học 2017-2018 phòng gd và đt quận Tây Hồ Hà Nội
- Đề khảo sát chất lượng toán 9 năm 2018 trường thpt chuyên Hà Nội Amsterdam
- Đề thi thử vào lớp 10 môn toán năm 2018 trường Chu Văn An Sơn La
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở gd và đt Hồ Chí Minh
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Thừa Thiên Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Quảng Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hưng Yên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Tây Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hải Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Ninh Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Quảng Ngãi
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Quảng Nam Chuyên Toán
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Chuyên Lê Quý Đôn Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Tiền Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Ptnk Tp Hồ Chí Minh không chuyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Thái Bình đề chuyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thpt Chuyên Thái Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hà Nội không chuyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Chuyên Khtn Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Nam Định Đề Chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường PTNK Tp Hcm Vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Chuyên Khtn Hà Nội vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường chuyên Đhsp Hà Nội đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bình Phước Chuyên Toán
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bình Phước đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt chuyên Lê Quý Đôn Bà Rịa Vũng Tàu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Lương Thế Vinh Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Mĩ Xá Nam Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Mạc Đĩnh Chi Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Nguyễn Công Trứ Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019 trường thcs Tân Mai Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Uông Bí Quảng Ninh
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Thái Thịnh Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Thăng Long Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Lương Thế Vinh Hà Nội Lần 3
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thpt Thăng Long Hà Nội Đợt 2
- Đề thi thử toán 9 năm 2019 trường thpt chuyên khtn Hà Nội vòng 2 Đợt 4
- Đề thi kscl vào lớp 10 Thpt năm 2018-2019 trường thcs Bạch Liêu Nghệ An
- Đề minh họa kì thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở gd và đt Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Nghệ An
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Quảng Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đà Nẵng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Vĩnh Long
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thừa Thiên Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thái Nguyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thái Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Sơn La
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Phú Thọ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Nam Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Long An
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lào Cai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lạng Sơn
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lâm Đồng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lai Châu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Kiên Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Khánh Hòa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hưng Yên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hậu Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hải Phòng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hà Tĩnh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hà Nam
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đồng Tháp
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đồng Nai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Điện Biên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đăk Nông
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bình Phước
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bến Tre
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bạc Liêu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bà Rịa Vũng Tàu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Tiền Giang
- Đề thi tuyển sinh vào lớp 10 chuyên môn toán năm học 2019-2020 sở gd và đt Gia Lai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Tây Ninh
- Đề thi tuyển sinh vào lớp 10 chuyên môn toán năm học 2019-2020 sở gd và đt Hưng Yên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hưng Yên đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thanh Hóa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Ninh Thuận
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hải Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán thpt chuyên năm học 2019-2020 sở gd và đt Hà Nam
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường PTNK tp Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường chuyên Thái Bình vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường chuyên Thái Bình vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường chuyên Lê Quý Đôn BRVT vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 thpt chuyên môn toán năm học 2019-2020 sở gd và đt Nam Định đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán chuyên năm học 2019-2020 sở gd và đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 phòng gd và đt Dương Kinh Hải Phòng lần 2
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường Lương Thế Vinh Hà Nội lần 4
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường Lương Ngọc Quyến Thái Nguyên
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 phòng gd và đt Chí Linh Hải Dương
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường thpt Hồng Hà Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 phòng gd và đt Lục Nam Bắc Giang
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường Trần Nhân Tông Hà Nội
- Đề minh họa tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Khánh Hòa
- Tuyển tập 50 đề luyện thi tuyển sinh lớp 10 thpt sở gd và đt Thái Bình
- Tuyển chọn các đề thi tuyển sinh vào lớp 10 môn toán Nguyễn Hoàng Nam
- Tuyển chọn 50 đề thi tuyển sinh vào lớp 10 chuyên môn toán
- PHÂN TÍCH VÀ BÌNH LUẬN MỘT SỐ ĐỀ THI VÀO LỚP 10 CHUYÊN CỦA MỘT SỐ TRƯỜNG TRÊN CẢ NƯỚC NĂM 2017
- Khảo sát toán tuyển sinh lớp 10 năm 2019-2020 trường Trương Công Định Hải Phòng
- Đề thi tuyển sinh vào lớp 10 môn toán của các trường chuyên trọn trên cả nước
- Đề thi thử vào lớp 10 môn toán phòng gd và đt Hải Hậu Nam Định lần 1
- Bộ đề ôn thi tuyển sinh vào lớp 10 thpt và thpt chuyên môn toán
- Đề Ôn Thi Vào Lớp 10 Môn Toán THCS Nguyễn Công Trứ 2021
- Đề Ôn Thi Vào Lớp 10 Môn Toán Phòng GDĐT Đan Phượng
- Tuyển tập đề thi vào 10 môn Toán sở GDĐT Hà Nội (từ 1998 đến 2020) có hướng dẫn giải
- ĐỀ THI VÀO 10 CHUYÊN KHTN VÒNG 2
- ĐỀ THI VÀO 10 CHÍNH THỨC SỞ HÀ NỘI MÔN TOÁN 2020-2021
- ĐỀ THI VÀO 10 CHÍNH THỨC SỞ HÀ NỘI MÔN TOÁN 2018-2019
- ĐỀ THI VÀO 10 CHÍNH THỨC SỞ HÀ NỘI 2020-2021
- ĐỀ THI TUYỂN SINH VÀO 10 MÔN TOÁN SỞ HÀ NỘI 2019-2020
- Đề thi thử vào lớp 10 môn Toán năm 2018 trường THPT Sơn Tây – Hà Nội
- Đề thi thử vào lớp 10 môn Toán năm 2018 trường Phan Huy Chú – Hà Nội
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT TRẦN NHÂN TÔNG
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT THĂNG LONG LẦN 2
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT THĂNG LONG HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT PHAN HUY CHÚ HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS VIỆT HÙNG
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS THANH TRÌ
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS THÀNH CÔNG HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS TÂN MAI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS KHƯƠNG THƯỢNG HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN SỞ GDĐT NAM ĐỊNH
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN PHÒNG GDĐT HOÀN KIẾM HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN PHÒNG GDDT GIA LÂM HÀ NỘI
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Xuân Canh Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Tam Khương Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Phòng GDDT Vĩnh Bảo Hải Phòng
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Phòng GDDT Huyện Lộc Bình Lạng Sơn
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường Chuyên ĐHSP Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Mĩ Đình 2 Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Khương Thượng Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Thành Công Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Khương Thượng Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THPT Hoàng Mai Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Nguyễn Công Trứ Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Trường THCS Nghinh Xuyên Phú Thọ
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Trường THCS Minh Phú Phú Thọ
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Lê Quý Đôn Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Nguyễn Công Trứ Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Nguyễn Du Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Thái Thịnh Hà Nội
- Đề Thi Thử Vào Lớp 10 Lần 2 Môn Toán Năm 2021 Trường Chuyên Đại Học Sư Phạm Hà Nội
- Đề Thi Thử Vào Lớp 10 Lần 2 Môn Toán Năm 2021-2022 Trường THCS Thái Thịnh Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Trường THCS Phan Huy Chú Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Lần 1 Trường THCS Kim Liên Nghệ An
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THPT Phan Huy Chú Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Sở GDDT Vĩnh Phúc
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Phòng GDDT Thạch Thành Thanh Hóa
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Phòng GDDT Gia Lâm Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2019-2020 Phòng GDDT Đan Phượng Hà Nội
- Bộ Đề Tham Khảo Tuyển Sinh Lớp 10 Năm 2020-2021 Môn Toán Sở GDDT HCM
Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 8)
đề thi môn toán vào 10
Môn thi: Toán (Công lập)
Thời gian làm bài: 120 phút
Bài 1 : ( 1,5 điểm) Cho hai biểu thức: (đề thi môn toán vào 10)
a) Rút gọn các biểu thức A và B
b) So sánh B với
Bài 2 : ( 1,5 điểm)Giải hệ phương trình sau:
Bài 3 : ( 2,5 điểm) (đề thi môn toán vào 10)
1) Cho phương trình: (m – 1)x2 – 2(m + 1)x + m = 0.
a) giải phương trình khi m = 2
b) Tìm m sao cho phương trình có 2 nghiệm x1; x2 phân biệt thỏa mãn điều kiện sau :
|x1 – x2| ≥ 2
2) giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Hai người dự định làm một công việc trong 12 giờ thì xong. Họ làm với nhau được 8 giờ thì người thứ nhất nghỉ, còn người thứ hai vẫn tiếp tục làm. Do cố gắng tăng năng suất gấp đôi nên người thứ hai đã làm xong xông việc còn lại trong 3 giờ 20 phút. Hỏi neeys mỗi người thợ làm một mình với năng suất dự định ban đầu thì mất bao lâu mới xong công việc nói trên?
Bài 4 : ( 3,5 điểm)
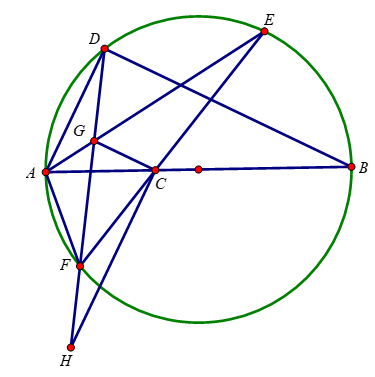
1. Trên đường tròn (O) đường kính AB, lấy điểm D (D ≠ A, D ≠ B). Gọi E là điểm chính giữa cung nhỏ BD. Lấy điểm C trên đoạn thẳng AB (C ≠ A, C ≠ B). Đường thẳng CE cắt đường tròn (O) tại điểm thứ hai là F. Gọi G là giao điểm của AE và DF.
a) Chứng minh ∠BAE = ∠DFE và AGCF là tứ giác nội tiếp.
b) Chứng minh CG vuông góc với AD.
c) Kẻ đường thẳng đi qua C, song song với AD và cắt DF tại H. Chứng minh CH = CB.
2. Một hình trụ có bán kính đáy bằng 2 cm và chiều cao bằng hai lần đường kính đáy. Tính thể tích của hình trụ đó.
Bài 5 : ( 1 điểm)
a) Cho x, y là các số thực dương. Chứng minh:
b) Cho a, b, c là các số thực dương. Chứng minh rằng:
Đáp án và Hướng dẫn giải
Bài 1 :
b) Xét biểu thức:
Do √x ≥ 0 nên
Bài 2 : (đề thi môn toán vào 10)
1) y = (m – 1)x + m + 3 với m ≠ -1 (m là tham số)
a) Hàm số đi qua điểm M (1; – 4) khi:
– 4 = (m – 1). 1 + m – 3
<=> 2m = 0 <=> m = 0
Vậy với m = 0 thì đồ thị hàm số đi qua điểm M ( 1; – 4)
b) Đồ thị của hàm số song song với đường thẳng (d): y = -2x + 1 khi và chỉ khi
Vậy với m = -1 thì đồ thị hàm số song song với đường thẳng (d): y = -2x + 1
2)
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (3; -9)
Bài 3 :
1) (m – 1)x2 – 2(m + 1)x + m = 0.
a) Khi m = 2,ta có phương trình:
x2 -6x + 2=0
∆’ = 32 – 2 = 7 > 0
Phương trình có 2 nghiệm phân biệt:
x1= 3 + √7
x2= 3 – √7
Vậy phương trình đã cho có tập nghiệm là: S = {3 + √7; 3 – √7}
b) (m – 1)x2 – 2(m + 1)x + m = 0.
Với m ≠ 1, ta có:
∆’ = (m + 1)2 – m(m – 1) = 3m + 1
Phương trình có 2 nghiệm phân biệt khi và chỉ khi:
Khi đó, theo định lí Vi-et, ta có:
Theo bài ra: |x1 – x2| ≥ 2
<=>(x1 – x2 )2 ≥ 4
<=>(x1 + x2 )2 – 4x1 x2 ≥ 4
=> (m + 1)2 – m(m – 1) – (m – 1)2 ≥ 0
<=> -m2 + 5m ≥ 0
<=> 0 ≤ m ≤5
Kết hợp với điều kiện thì các giá trị của m thỏa mãn đề bài là
2) Đổi 3 giờ 20 phút = 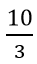
Gọi số giờ người thứ nhất làm một mình xong công việc với năng suất ban đầu là x (giờ)
=> Trong 1 giờ,người thứ nhất làm được 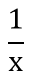
Gọi số giờ người thứ hai làm một mình xong công việc với năng suất ban đầu là y (giờ)
=> Trong 1 giờ,người thứ hai làm được 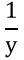
=> Trong 1 giờ,cả hai người làm được 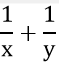
Theo bài ra, 2 người làm chung trong 12 giờ thì xong công việc nên ta có phương trình
Người thứ hai làm việc với năng suất gấp đôi nên trong 1 giờ người thứ hai làm được: 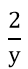
Trong 3 giờ 20 phút, người thứ hai làm việc với năng suất gấp đôi nên người đó đã làm được:
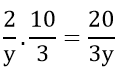
Họ làm với nhau được 8 giờ thì người thứ nhất nghỉ, còn người thứ hai vẫn tiếp tục làm. Do cố gắng tăng năng suất gấp đôi nên người thứ hai đã làm xong xông việc còn lại trong 3 giờ 20 phút nên ta có phương trình:
Theo bài ra ta có hệ phương trình:
Vậy người thứ nhất làm một mình với năng suất ban đầu thì làm xong công việc trong 30 giờ.
Người thứ hai làm một mình với năng suất ban đầu thì làm xong công việc trong 20 giờ.
Bài 4 :
1)
a) Xét đường tròn (O), ta có:
⏜
BE = DE(E là điểm chính giữa cung BD)
=> BAE = DFE (2 góc nội tiếp chắn 2 cung bằng nhau)
Xét tứ giác AGCF có:
∠GAC = ∠GFC (cmt)
=> 2 đỉnh A và F cùng nhìn cạnh GC dưới 2 góc bằng nhau
=>Tứ giác AGCF là tứ giác nội tiếp.
b) Tứ giác AGCF là tứ giác nội tiếp
=> ∠CGF = ∠CAF (2 góc nội tiếp cùng chắn cung CF)
Mà ∠CAF = ∠FDB (2 góc nội tiếp cùng chắn cung FB)
=> ∠CGF = ∠FDB
2 góc này ở vị trí đồng Vị
=> BD // GC
Mà BD ⊥ AD ( ∠ADB = 90o,góc nội tiếp chắn nửa đường tròn)
=> GC ⊥ AD
c) Gọi M là giao điểm của AB và DF
Do CH // AD nên ta có:
Mặt khác, ta lại có: CG // BD nên:
Từ (1), (2) và (3) => CH = CB
2. Hình nón có bán kính đáy R = 2 cm
Chiều cao bằng hai lần đường kính đáy nên chiều cao của hình nón là: h = 2.2.2 = 8 cm
Thể tích của hình nón là:
Bài 5 :
a)
Với x, y > 0 ta có:
<=> (x + y)2 – 4xy ≥ 0
<=> (x – y)2 ≥ 0 ( luôn đúng)
b)
Do a, b, c là các số thực dương nên a + 3b > 0, b + 2c + a > 0
Theo câu a, ta có:
Tương tự, ta có:
Một số đề thi vào lớp 10 khác: