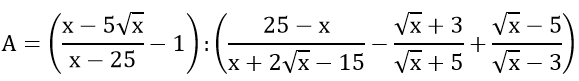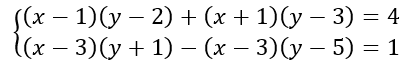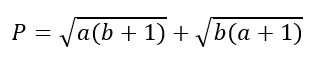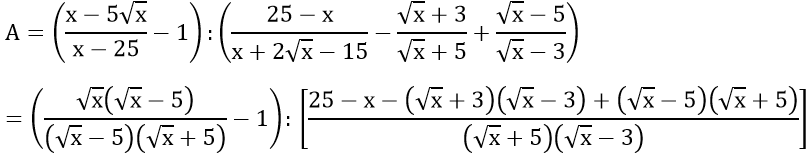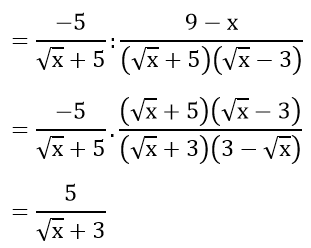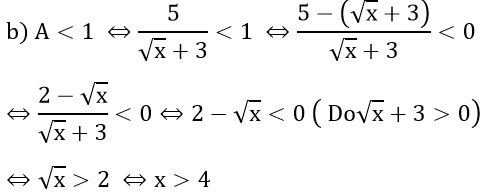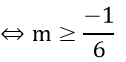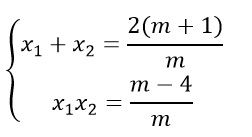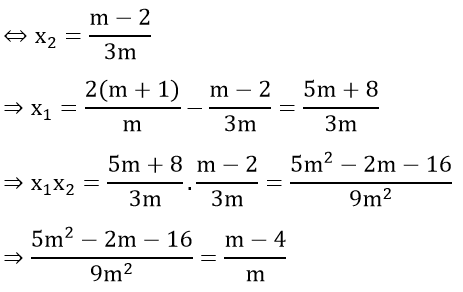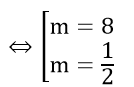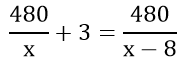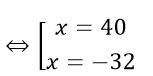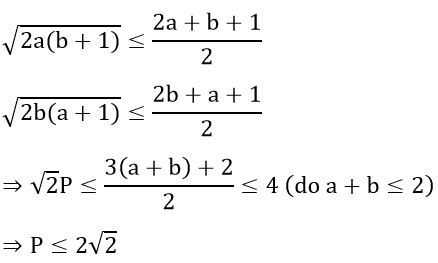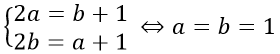- Tuyển tập 60 đề thi vào 10 các sở giáo dục có đáp án chi tiết
- Tuyển tập đề thi vào 10 năm học 2017-2018
- Đề thi môn Toán vào 10 (có đáp án – Đề 1)
- Đề thi môn Toán vào 10 (có đáp án – Đề 2)
- Đề thi môn Toán vào 10 (có đáp án – Đề 3)
- Đề thi môn Toán vào 10 (có đáp án – Đề 4)
- Đề thi môn Toán vào 10 (có đáp án – Đề 5)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 1)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 2)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 3)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 4)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 5)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 6)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 7)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 8)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 9)
- Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 10)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 1)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 2)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 3)
- Đề thi môn Toán vào 10 thành phố hà nội (có đáp án – Đề 4)
- Đề thi thử vào 10 THPT thăng long lần 2 năm 2019
- TUYỂN TẬP ĐỀ THI VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2017-2018
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Lê Quý Đôn Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở gd và đt Vĩnh Phúc
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Tiền Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Thừa Thiên Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Thanh Hóa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Phú Thọ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Ninh Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Nam Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Long An
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Lạng Sơn
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hải Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hà Nội Chuyên Tin
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Hà Nam
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đồng Nai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đà Nẵng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Thành Phố Cần Thơ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bình Phước
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt An Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bến Tre
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 Trường Thpt Chuyên Lê Quý Đôn Bình Định Chuyên Toán
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Chuyên Vĩnh Phúc
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Vĩnh Long
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Quảng Ngãi
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Lâm Đồng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Lai Châu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Đồng Tháp
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Lương Thế Vinh Đồng Nai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên An Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Bà Rịa Vùng Tàu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Lạc Thủy Hòa Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên quốc học Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Quốc Học Huế Chuyên Toán
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Quốc Học Huế chuyên tin
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Lam Sơn Thanh Hóa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên KHTN Hà Nội vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên KHTN Hà Nội Vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Hùng Vương Phú Thọ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên Hùng Vương Phú Thọ chuyên tin
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên đh Sư Phạm vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt chuyên đh Sư Phạm Hà Nội Vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Thực Hành Cao Nguyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở Gd và Đt Tây Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 Phòng Gd và Đt Giao Thủy
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Sơn Tây Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Nhân Chính Thanh Xuân
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường Thpt Phan Huy Chú Đống Đa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường Thcs Thái Thịnh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2017-2018 cụm trường Thcs Quận Hai Bà Trưng
- Đề thi thử vào lớp 10 môn toán năm học 2017-2018 trường THCS ARCHIMEDES ACADEMY lần 6
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Lương Thế Vinh Hồ Chí Minh
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs An Đà Hải Phòng Lần 1
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 sở gd và đt Tam Đảo
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường Thpt Thăng Long Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thpt Đào Duy Từ Thanh Hóa
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Võ Thị Sáu Hải Phòng
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Thiệu Vận Thanh Hóa Lần 1
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2017-2018 trường thcs Nga Thiện Thanh Hóa
- Đề thi thử toán 9 năm 2018 trường thpt Chuyên khtn Hà Nội vòng 1 đợt 1
- Đề thi khảo sát toán 9 năm học 2017- 2018 phòng gd và đt Ba Đình Hà Nội
- Đề kscl Toán 9 năm học 2017-2018 phòng gd và đt Vĩnh Tường Vĩnh Phúc
- Đề kscl toán 9 năm học 2017-2018 phòng gd và đt Thanh Trì Hà Nội Lần 2
- Đề kscl toán 9 năm học 2017-2018 trường thcs Lê Quý Đôn Hà Nội Lần 2
- Đề kiểm tra giữa học kì 2 toán 9 toán 9 năm học 2017-2018 phòng gd và đt quận Tây Hồ Hà Nội
- Đề khảo sát chất lượng toán 9 năm 2018 trường thpt chuyên Hà Nội Amsterdam
- Đề thi thử vào lớp 10 môn toán năm 2018 trường Chu Văn An Sơn La
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở gd và đt Hồ Chí Minh
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Thừa Thiên Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Quảng Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hưng Yên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Tây Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hải Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Ninh Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Quảng Ngãi
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Quảng Nam Chuyên Toán
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Chuyên Lê Quý Đôn Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Tiền Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Ptnk Tp Hồ Chí Minh không chuyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Thái Bình đề chuyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thpt Chuyên Thái Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Hà Nội không chuyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Chuyên Khtn Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Nam Định Đề Chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường PTNK Tp Hcm Vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Chuyên Khtn Hà Nội vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường chuyên Đhsp Hà Nội đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bình Phước Chuyên Toán
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở Gd và Đt Bình Phước đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt chuyên Lê Quý Đôn Bà Rịa Vũng Tàu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Lương Thế Vinh Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Mĩ Xá Nam Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Mạc Đĩnh Chi Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Nguyễn Công Trứ Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019 trường thcs Tân Mai Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Uông Bí Quảng Ninh
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thcs Thái Thịnh Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Thpt Thăng Long Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường Lương Thế Vinh Hà Nội Lần 3
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2018-2019 trường thpt Thăng Long Hà Nội Đợt 2
- Đề thi thử toán 9 năm 2019 trường thpt chuyên khtn Hà Nội vòng 2 Đợt 4
- Đề thi kscl vào lớp 10 Thpt năm 2018-2019 trường thcs Bạch Liêu Nghệ An
- Đề minh họa kì thi tuyển sinh vào lớp 10 môn toán năm học 2018-2019 sở gd và đt Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Nghệ An
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Quảng Ninh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đà Nẵng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Vĩnh Long
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thừa Thiên Huế
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thái Nguyên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thái Bình
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Sơn La
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Phú Thọ
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Nam Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Long An
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lào Cai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lạng Sơn
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lâm Đồng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Lai Châu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Kiên Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Khánh Hòa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hưng Yên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hậu Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hải Phòng
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hà Tĩnh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hà Nam
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đồng Tháp
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đồng Nai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Điện Biên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đăk Nông
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bình Phước
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bình Định
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bến Tre
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bạc Liêu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bà Rịa Vũng Tàu
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Tiền Giang
- Đề thi tuyển sinh vào lớp 10 chuyên môn toán năm học 2019-2020 sở gd và đt Gia Lai
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Tây Ninh
- Đề thi tuyển sinh vào lớp 10 chuyên môn toán năm học 2019-2020 sở gd và đt Hưng Yên
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hưng Yên đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Thanh Hóa
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Ninh Thuận
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hải Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bắc Giang
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán thpt chuyên năm học 2019-2020 sở gd và đt Hà Nam
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hà Nội
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường PTNK tp Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường chuyên Thái Bình vòng 2
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường chuyên Thái Bình vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường chuyên Lê Quý Đôn BRVT vòng 1
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Hồ Chí Minh
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Bắc Ninh
- Đề thi tuyển sinh vào lớp 10 thpt chuyên môn toán năm học 2019-2020 sở gd và đt Nam Định đề chung
- Đề thi tuyển sinh vào lớp 10 môn toán chuyên năm học 2019-2020 sở gd và đt Đăk Lăk
- Đề thi tuyển sinh vào lớp 10 môn toán năm học 2019-2020 phòng gd và đt Dương Kinh Hải Phòng lần 2
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường Lương Thế Vinh Hà Nội lần 4
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường Lương Ngọc Quyến Thái Nguyên
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 phòng gd và đt Chí Linh Hải Dương
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường thpt Hồng Hà Hà Nội
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 phòng gd và đt Lục Nam Bắc Giang
- Đề thi thử tuyển sinh vào lớp 10 môn toán năm học 2019-2020 trường Trần Nhân Tông Hà Nội
- Đề minh họa tuyển sinh vào lớp 10 môn toán năm học 2019-2020 sở gd và đt Khánh Hòa
- Tuyển tập 50 đề luyện thi tuyển sinh lớp 10 thpt sở gd và đt Thái Bình
- Tuyển chọn các đề thi tuyển sinh vào lớp 10 môn toán Nguyễn Hoàng Nam
- Tuyển chọn 50 đề thi tuyển sinh vào lớp 10 chuyên môn toán
- PHÂN TÍCH VÀ BÌNH LUẬN MỘT SỐ ĐỀ THI VÀO LỚP 10 CHUYÊN CỦA MỘT SỐ TRƯỜNG TRÊN CẢ NƯỚC NĂM 2017
- Khảo sát toán tuyển sinh lớp 10 năm 2019-2020 trường Trương Công Định Hải Phòng
- Đề thi tuyển sinh vào lớp 10 môn toán của các trường chuyên trọn trên cả nước
- Đề thi thử vào lớp 10 môn toán phòng gd và đt Hải Hậu Nam Định lần 1
- Bộ đề ôn thi tuyển sinh vào lớp 10 thpt và thpt chuyên môn toán
- Đề Ôn Thi Vào Lớp 10 Môn Toán THCS Nguyễn Công Trứ 2021
- Đề Ôn Thi Vào Lớp 10 Môn Toán Phòng GDĐT Đan Phượng
- Tuyển tập đề thi vào 10 môn Toán sở GDĐT Hà Nội (từ 1998 đến 2020) có hướng dẫn giải
- ĐỀ THI VÀO 10 CHUYÊN KHTN VÒNG 2
- ĐỀ THI VÀO 10 CHÍNH THỨC SỞ HÀ NỘI MÔN TOÁN 2020-2021
- ĐỀ THI VÀO 10 CHÍNH THỨC SỞ HÀ NỘI MÔN TOÁN 2018-2019
- ĐỀ THI VÀO 10 CHÍNH THỨC SỞ HÀ NỘI 2020-2021
- ĐỀ THI TUYỂN SINH VÀO 10 MÔN TOÁN SỞ HÀ NỘI 2019-2020
- Đề thi thử vào lớp 10 môn Toán năm 2018 trường THPT Sơn Tây – Hà Nội
- Đề thi thử vào lớp 10 môn Toán năm 2018 trường Phan Huy Chú – Hà Nội
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT TRẦN NHÂN TÔNG
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT THĂNG LONG LẦN 2
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT THĂNG LONG HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THPT PHAN HUY CHÚ HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS VIỆT HÙNG
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS THANH TRÌ
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS THÀNH CÔNG HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS TÂN MAI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN THCS KHƯƠNG THƯỢNG HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN SỞ GDĐT NAM ĐỊNH
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN PHÒNG GDĐT HOÀN KIẾM HÀ NỘI
- ĐỀ THI THỬ VÀO 10 MÔN TOÁN PHÒNG GDDT GIA LÂM HÀ NỘI
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Xuân Canh Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Tam Khương Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Phòng GDDT Vĩnh Bảo Hải Phòng
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Phòng GDDT Huyện Lộc Bình Lạng Sơn
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường Chuyên ĐHSP Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Mĩ Đình 2 Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Khương Thượng Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Thành Công Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Khương Thượng Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THPT Hoàng Mai Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Nguyễn Công Trứ Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Trường THCS Nghinh Xuyên Phú Thọ
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Trường THCS Minh Phú Phú Thọ
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Lê Quý Đôn Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Nguyễn Công Trứ Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Nguyễn Du Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THCS Thái Thịnh Hà Nội
- Đề Thi Thử Vào Lớp 10 Lần 2 Môn Toán Năm 2021 Trường Chuyên Đại Học Sư Phạm Hà Nội
- Đề Thi Thử Vào Lớp 10 Lần 2 Môn Toán Năm 2021-2022 Trường THCS Thái Thịnh Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Trường THCS Phan Huy Chú Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Lần 1 Trường THCS Kim Liên Nghệ An
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Trường THPT Phan Huy Chú Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Sở GDDT Vĩnh Phúc
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2021-2022 Phòng GDDT Thạch Thành Thanh Hóa
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2020-2021 Phòng GDDT Gia Lâm Hà Nội
- Đề Thi Thử Vào Lớp 10 Môn Toán Năm 2019-2020 Phòng GDDT Đan Phượng Hà Nội
- Bộ Đề Tham Khảo Tuyển Sinh Lớp 10 Năm 2020-2021 Môn Toán Sở GDDT HCM
Đề thi môn Toán vào 10 (có đáp án – Tự luận – Đề 3)
đề thi môn toán vào 10
Môn thi: Toán (Công lập)
Thời gian làm bài: 120 phút
Bài 1 : ( 2 điểm)Cho biểu thức: (đề thi môn toán vào 10)
với x ≥ 0; x ≠ 9,x ≠ 25
a) Rút gọn A.
b) Tìm x để A < 1.
Bài 2 : ( 2 điểm) (đề thi môn toán vào 10)
1) Cho Phương trình: mx2 – 2(m + 1)x + (m – 4) = 0 (m là tham số).
a) Xác định m để các nghiệm x1; x2 của Phương trình thoả mãn x1 + 4x2 = 3
b) Tìm một hệ thức giữa x1; x2 mà không phụ thuộc vào m
2) giải hệ phương trình
Bài 3 : ( 2 điểm)Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Lớp 9A được phân công trồng 480 cây xanh. Tuy nhiên, khi lao động có 8 bạn vắng nên mỗi bạn có mặt phải trồng thêm 3 cây mới xong. Biết rằng số cây mỗi học sinh trồng như nhau. Hỏi lớp 9A có bao nhiêu học sinh?
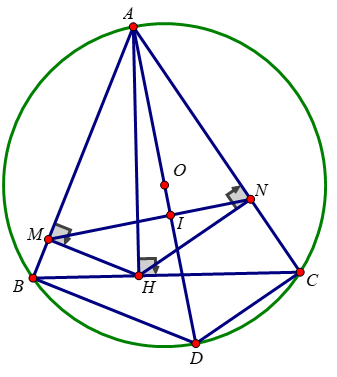
Bài 4 : ( 3,5 điểm)Cho tam giác ABC nhọn nội tiếp đường tròn (O; R). AH là đường cao của tam giác ABC, M, N theo thứ tự là hình chiếu của H trên AB, AC.
a) Chứng minh AMHN là tứ giác nội tiếp
b) Chứng minh (ABC) =(ANM)
c) Chứng minh OA ⊥ MN
d) Khi AH = 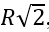
Bài 5: ( 0,5 điểm) Cho a, b > 0 và a + b =< 2. Tìm giá trị nhỏ nhất của biểu thức
Đáp án và Hướng dẫn giải
Bài 1:
a) Với x ≥ 0; x ≠ 9, x ≠ 25
Vậy với x > 4; x ≠ 9, x ≠ 25 thì A <
Bài 2: (đề thi môn toán vào 10)
a) Với m ≠ 0, phương trình trên là phương trình bậc hai ẩn x
Δ’ = (m + 1)2 – m(m – 4) = m2 + 2m + 1 – m2 + 4m = 6m + 1
Phương trình có 2 nghiệm x1; x2 khi và chỉ khi Δ’ = 6m + 1 ≥ 0
Khi đó, theo định lí Vi-et ta có:
Theo bài ra:
x1 + 4x2 = 3
<=> (x1 + x2 ) + 3x2 = 3
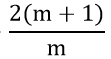
=> 5m2 – 2m – 16 = 9m2 – 36m
<=> 4m2 – 34m + 16 = 0
Đối chiếu với điều kiện thỏa mãn
Vậy m = 8, m = 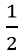
b) Ta có:
2(x1 + x2 ) + x1x2 = 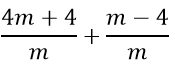
Vậy hệ thức liên hệ giữa x1 và x2 không phụ thuộc vào m là 2(x1 + x2 ) + x1x2 = 5
Bài 3:
Gọi số học sinh lớp 9A là x ( học sinh) (x > 8, x ∈ N)
Khi đó, số cây mỗi học sinh phải trồng là:
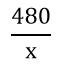
Do có 8 bạn học sinh vắng mặt nên số cây mỗi bạn phải trồng là
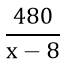
Theo bài ra, mỗi bạn phải trồng thêm 3 cây nên ta có phương trình
=> 480(x – 8) + 3x(x – 8) = 480x
<=> 3x2 – 24x – 3840 = 0
Vậy số học sinh lớp 9A là 40 học sinh
Bài 4:
a) Xét tứ giác AMHN có:
∠AMH = 90o (MH ⊥ AB)
∠ANH = 90o (NH ⊥ AC)
=> ∠AMH + ∠ANH = 180o
=> Tứ giác AMHN là tứ giác nội tiếp
b) Ta có:
ΔAMH vuông tại M: ∠AHM + ∠MAH = 90o
ΔABH vuông tại H: ∠ABC + ∠MAH = 90o
=> ∠AHM = ∠ABC
Do tứ giác AMHN là tứ giác nội tiếp nên ∠AHM = ∠ANM (2 góc nội tiếp cùng chắn cung AM)
=> ∠ABC = ∠ANM
c) Kẻ đường kính AD của (O), Gọi I là giao điểm của AD và MN
ΔANH vuông tại N: ∠AHN + ∠NAH = 90o
ΔACH vuông tại H: ∠AHN + ∠ACB = 90o
=> ∠NAH = ∠ACB
Ta lại có: ∠ACB = ∠ADB (2 góc nội tiếp cùng chắn cung AB)
=> ∠NAH = ∠ADB
Mặt khác: tứ giác AMHN là tứ giác nội tiếp nên ∠AMN = ∠AHN (2 góc nội tiếp cùng chắn cung AN)
=> ∠AMN = ∠ADB
Xét ΔAMI và ΔABD có:
∠BAD là góc chung
∠AMN = ∠ADB
=> ΔAMI ∼ ΔADB
=> ∠ AIM = ∠ABD
Mà ∠ABD = 90o (góc nội tiếp chắn nửa đường tròn)
=> ∠AIM = 90o
Hay OA ⊥ MN
d) Xét tam giác AIN và tam giác ACD có:
∠DAC là góc chung
∠AIN = ∠ACD = 90o
=> ΔAIN ∼ ΔACD
=>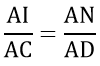
Xét ΔAHC vuông tại H có HN là đường cao
=> AC. AN = AH2 (2)
Từ (1) và (2) => AI.AD = AH2 <=> AI.AD = 2R2
<=> AI.2R = 2R2 <=> AI = R <=> I ≡ O
Vậy M, N, O thẳng hàng.
Bài 5:
Do a, b > 0 nên ta có:
Dấu bằng xảy ra khi:
Vậy GTLN của P là 2√2, đạt được khi a = b = 1.